200�X�N�@���s��w�i���n�j�E�O���@���Ɖ�
�@
|
�@�P�D�@���̊e��ɂ��ꂼ�ꓚ����B �@�@(1)�@ xyz��ԏ��2�_A�i�|3�C�|1�C1�j�CB�i�|1�C0�C0�j��ʂ钼��l�ɓ_C�i2�C3�C3�j���牺�낵 �@�@�@�@�������̑�H�̍��W�����߂�B �@�@(2)�@�����Ɛԋ��̓������܂���2�̋����Ɏ��o���Q�[�����l����B���o����2���� �@�@�@�@�Ƃ��ɔ����Ȃ�u�����v�ŃQ�[�����I�����C�����łȂ��Ƃ��́u���s�v�Ƃ��C���o����2���� �@�@�@�@�ԋ���1������3�̋���܂ɂ��ǂ��ăQ�[���𑱂�����̂Ƃ���B�ŏ��ɔ�����2�C �@�@�@�@�ԋ���1�܂ɓ����Ă����Ƃ��Cn�|1��܂Ŏ��s��n��ڂɐ�������m�������߂�B�������C �@�@�@�@n��2�Ƃ���B |
[��]�@
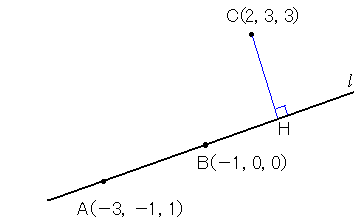
(1)�@
�@�@
![]()
![]()
![]()
�@�@CH��AB������C�����ρ��O���g���B
�@�@�@�@�@�@�@�@�@�@2�i2t�|5�j�{�it�|4�j�|�i�|t�|2�j��0
6t�|12��0
t��2
![]()
�@�@�i���j�@�i1�C1�C�|1�j
(2)�@k��1�C2�C3�C�E�E�E�Cn�|1�Ƃ���B
�@�@k��ڂł́C�܂̒��ɔ���2�C�ԋ�k�������Ă���B���̉�Ɏ��s����m���́C
�@�@�����ȊO�����o���m���B
�@�@�@![]()
�@�@�@�@�@�@�@�@�@![]()
�@�@�@�@�@�@�@�@�@![]()
�@�@�܂��Cn��ڂł́C�܂̒��ɔ���2�C�ԋ�n�������Ă���B���̉�ɐ�������m���́C
�@�@���������o���m���B�@
�@�@�@�@�@![]()
�@�@����āC���߂�m���́C����̊m���̑S���̐�
�@�@�@�@�@![]()
�@�@�@�@![]()
�@�@�@�@![]()
�@�@�@�@![]()
�@�@![]()
|
�@�Q�D�@����f�ix�j�Ǝ���C�� �@�@�@�@�@�@�@�@�@ �@�@�@���݂����Ƃ��C����f�ix�j��C�����߂�B �@�@�@�@�@�@ |
[��]�@
������ό`����ƁC��x��ϕ��̊O�ɏo���Ă����B
�@�@�@![]()
���ӂ�x�Ŕ�������ƁC���܂������������Ȃ�B
�@�@�@![]()
![]()
�@�@�@�@�@![]()
�@�@�@�@�@�@![]()
�����ŁC��f ��A�CB�ɑ������B
�@�@�@![]()
�@�@�@�@�@![]()
������C�@2A�{2B��1�@�E�E�E�E�E�E�@
�@�@�@![]()
�@�@�@�@![]()
������C�@A�{3B��1�@�E�E�E�E�E�E�A
�@�C�A���C
�@�@�@![]()
�@�@�@![]()
�܂��C����x��0��������ƁC�������C���킩��B
�@�@![]()
�@�@�@![]()
![]()
|
�@�R�D�@x�Cy��x��1�Cy��1���݂������̐��ŁC�s�����@ �@�@�@�@�@�@�@�@�@log x y�{log y x��2�{�ilog x 2�j�ilog y 2�j �@�@���݂����Ƃ���B���̂Ƃ�x�Cy�̑g�ix�Cy�j�͈̔͂����W���ʏ�ɐ}������B |
[��]�@
�@�@�@log x y�{log y x��2�{�ilog x 2�j�ilog y 2�j
���2�Ƃ��āC��̕\�L�͏ȗ�����B���܂��͒�����낦��B
�@�@�@![]()
�@�@�@![]()
�@�@�@![]()
���ӂɐ��̐��ilog x�Elog y�j2 ���|���āC
log x�Elog y�ilog x�|log y�{1�j�ilog x�|log y�|1�j��0
�����ŁC���̈�̋��E���ׂ�B
�@�@log x��0�̂Ƃ��Cx��1
log y��0�̂Ƃ��Cy��1
![]()
![]()
�i���j�}�̉��̕����B���E�͊܂܂Ȃ��B���S�̋��E���������Ă����C���݂ɐF���ʂ�B
�@�@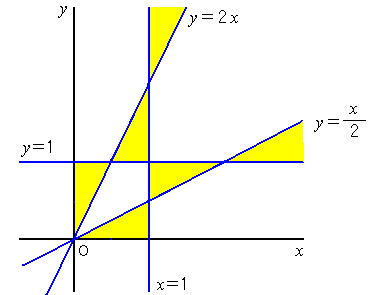
|
�@�S�D�@���ʏ�ŁC�s�p�O�p�`��OAB���OB�Ɋւ��Đ܂�Ԃ��ē�����O�p�`����OBC�C �@�@�@��OBC���OC�Ɋւ��Đ܂�Ԃ��ē�����O�p�`����OCD�C��OCD���OD�Ɋւ��� �@�@�@�܂�Ԃ��ē�����O�p�`����ODE�Ƃ���B��OAB�Ɓ�OBE�̖ʐϔ䂪2�F3�̂Ƃ��C �@�@�@sin��AOB�̒l�����߂�B |
[��]�@
��AOB���ƁCOA��a�COB��b�Ƃ���ƁC
�@�@![]()
3�Ɓ��̂Ƃ��́�OBE�͂ł��Ȃ��B����ȊO�̂Ƃ��͎��̂悤�ɂȂ�B���ꍇ����������̂��������肵�₷���B
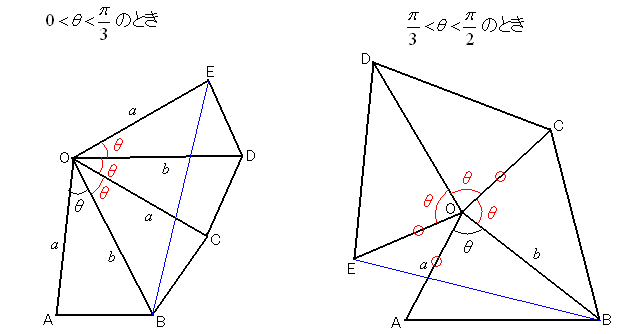
�ǂ���̏ꍇ���C
�@�@�@�@![]()
�@�@�@�@�@�@�@�@�@![]()
�@�@�@�@�@�@�@�@�@![]()
�@�@�@�@�@�@�@�@�@![]()
���Ƃ͐�Βl�̒����l�����OK�B
![]()
�@�@�@�@�@�@![]()
0��sin2�Ɓ�1���C�|1��3�|4sin2�Ɓ�3������C���P�Ɍ��肳���B
�@�@�@�@�@�@![]()
![]()
�@�@�@ �@�@�@![]()
![]()
|
�@�T�D�@p��f���Cn�𐳂̐����Ƃ���Ƃ��C�i
p n �j�I��p�ʼn����邩�B |
[��]�@
�i p n �j�I��1�E2�E3�E�E�E�E�E�Ep n
�P����p n�܂ł̐������ׂĂɂ��āCp�̈����̌������߂�悢�B
p�̔{���́C�@�@�@�@�@1�Ep�C2p�C3p�C�E�E�E�Cp n�|1�Ep������C p n�|1�B�@
p2�̔{���́C�@�@�@�@�@1�Ep2�C2p2�C3p2�C�E�E�E�Cp n�|2�Ep2������C p n�|2�B�@
�E�E�E�E�E�E�E�E�E�E�E�E
p n�|1�̔{���́C�@�@�@1�Ep n�|1�C2 p n�|1�C3 p n�|1�C�E�E�E�Cp�Ep n�|1������C p�B�@
p n�̔{���́C�@�@�@�@ p n �݂̂ŁC 1�B�@
���̒��ɂ͏d�������������邪�Cp�̈����̌��͂����̘a�ŋ��܂�B
���̍��v�́C
�@�@�@p n�|1�{p n�|2�{�E�E�E�{p�{1
���ꂪ�C�i p n �j�I��p�ʼn����邩��\�����ł���B
�@�@�@![]()
![]()
�@