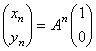200�X�N�@���s��w�i���n���j�E�O���@���Ɖ�
�@
|
�@�P�D�@xyz��Ԃ�O�i0�C0�C0�j�CA�i3�C0�C0�j�CB�i3�C2�C0�j�CC�i0�C2�C0�j�CD�i0�C0�C4�j�CE�i3�C0�C4�j�C F�i3�C2�C4�j�CG�i0�C2�C4�j�_�Ƃ��钼����OABC-DEFG���l����B��AE��s�F1�|s�ɓ������� �@�@�_��P�C��CG��t�F1�|t�ɓ�������_��Q�Ƃ����B������0��s��1�C0��t��1�Ƃ���B �@�@D��ʂ�CO�CP�CQ���܂ޕ��ʂɐ����Ȓ���������AC�i���[���܂ށj�ƌ����悤��s�Ct�݂̂��� �@�@���������߂�B |
[��]�@
�@�@�@![]()
�@�@�@![]()
D��ʂ蕽��OPQ�ɐ����Ȓ������C����AC�ƌ����_��R�Ƃ���B
AR�FRC��u�F1�|u�@�i0��u��1�j�@�Ƃ���ƁC
�@�@�@![]()
�@�@�@![]()
����ŁC���V�������ׂĂ�������B
DR�ہi����OPQ�j������CDR��OP�CDR��OQ
�@�@�@�@�@�@9u�|16s��0�@�@���i���ρj���O������B
�@�@�@4(1�|u )�|16t��0
���������C
�@�@�@�@�@�@9u��16s
�@�@�@ u��1�|4t
![]()
�����������Ƃ��́C���͈̔͂f�����悤�B
u����������ƁC 16s��9(1�|4t )
���Ȃ킿�C�@�@�@�@16s�{36 t��9
![]()
|
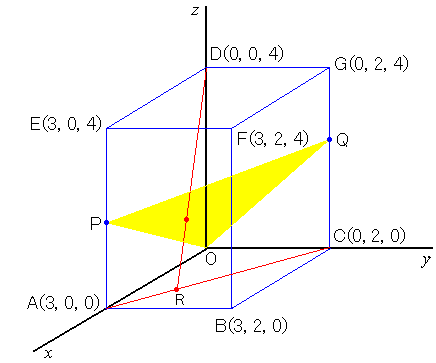
�@�Q�D�@���ʏ�̉s�p�O�p�`��ABC�̓����i�ӂⒸ�_�͊܂܂Ȃ��j�ɓ_P���Ƃ�CA�L��B�CC�CP�� �@�@�@�ʂ�~�̒��S�CB�L��C�CA�CP��ʂ�~�̒��S�CC�L��A�CB�CP��ʂ�~�̒��S�Ƃ���B �@�@�@���̂Ƃ�A�CB�CC�CA�L�CB�L�CC�L������~����ɂ��邽�߂̕K�v�\��������P����ABC�̓��S �@�@�@�Ɉ�v���邱�Ƃł��邱�Ƃ������B �@�@�@�@�@�@ |
[��]�@
�������}�ł��ˁB�ǂ�����Ď�����E�E�B
��PBC��b�C��PCB��c �Ƃ���ƁC�~A�L�̉~���p�ƒ��S�p�̊W����C
�@�@��P A�LB��2 c�C��P A�LC��2b
��A�LBC�L�߁�A�LPC�L������C��B A�LC�L����P A�LC�L��c�@���Ƃ肠�����p�x��ݒ肵�Ă����B
���l�ɁC
��A�LCB�L�߁�A�LPB�L������C��C A�LB�L����P A�LB �L��b
��AC�LB�L�߁�P C�LB�L������CAP��C�LB�L�@�E�E�E�E�E�E�@�@�����ꂪ���Ƃł����Ă���B
�k�T�l�@A�CB�CC�CA�L�CB�L�CC�L������~��S��ɂ���@�ˁ@P����ABC�̓��S�Ɉ�v����
�@�������B
�@�~S�̉~���p�̊W����C��B A�LC�L����B AC�L��c�C��C A�LB�L����C AB�L��b
�@����ɁCC�LA��C�LB�C B�LA��B�LC������C
�@�@�@�@��C�LA B����C�LB A����AB�LC�L��c�@���~���p���t���Ɋ��p���悤�B
�@�@�@�@��B�LA C����B�LCA����A C�LB�L��b�@
�@C�LB�L��AB�CAC�Ƃ̌�_�����ꂼ��Q�CR�Ƃ���ƁC
�@�@�@�@��A QR����ARQ��b�{c�@�E�E�E�E�E�E�A
�@�@�C�A���CAP�́�BAC�̓����ł���B�@�����S�̒�`�ƂȂ��Ă���B
�@
�@��̏ؖ��̌�����ς��Ď������Ƃœ��l�ɂ��āC
�@�@�@BP�́�ABC�̓����CCP�́�ACB�̓���
�@�ł��邱�Ƃ����ꂼ�ꌾ����B
�@����āC�_P�́�ABC�̓��S�ł���B
�k�U�l�@P����ABC�̓��S�Ɉ�v����@�ˁ@A�CB�CC�CA�L�CB�L�CC�L������~����ɂ���@�@
�@�������B��������͂���Ȃɓ���Ȃ��B
�@P����ABC�̓��S������C��ABP����PBC��b�C��ACP����BCP��c
�@��ABC�̓��p������C�@��BAC��180���|�i2 b�{2 c�j
�@�l�p�`ABA�LC�̓��p�ɂ����āC�@�������������p�̘a�ׂ�B
�@�@�@�@��BAC�{��BA�LC��180���|�i2 b�{2 c�j�{�i2 b�{2 c�j��180��
�@����āC�l�p�`ABA�LC�͉~�ɓ��ڂ���B���̉~�́�ABC�̊O�ډ~�ł���B
�@
�@��̏ؖ��̌�����ς��Ď������Ƃœ��l�ɂ��āC
�@�@�@�l�p�`AB CB�L�͉~�ɓ��ڂ���
�@�@�@�l�p�`CAC�LB�͉~�ɓ��ڂ���
�@���Ƃ����ꂼ�ꌾ����B�����̉~�͂Ƃ��Ɂ�ABC�̊O�ډ~�ł���B
�@
�@����āCA�CB�CC�CA�L�CB�L�CC�L�͓���~����ɂ����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�ؖ��I���j
|
�@�R�D�@n���̃J�[�h��ςR������C�e�J�[�h�ɂ͏ォ�珇�Ԃ�1����n�܂Ŕԍ��������� �@�@�@����B������n��2�Ƃ���B���̃J�[�h�̎R�ɑ��Ď��̎��s���J��Ԃ��B1��̎��s�ł́C �@�@�@��ԏ�̃J�[�h�����C�R�̈�ԏ�ɂ��ǂ����C���邢�͂����ꂩ�̃J�[�h�̉��ɓ����Ƃ� �@�@�@��������s���B�����n�ʂ�̑���͂��ׂē����m���ł���Ƃ���Bn��̎��s���I�����Ƃ��C �@�@�@�ŏ���ԉ��ɂ������J�[�h�i�ԍ�n�j���R�̈�ԏ�ɂ��Ă���m�������߂�B |
[��]�@
n��̎��s�ɂ���Ăł���J�[�h�̈ړ��̑�����n n�ʂ�ŁC�����͓��l�Ɋm���炵���B�����ŁC
n��̎��s��C�ԍ�n�̃J�[�h���R�̈�ԏ�ɗ���悤�Ȉړ��̑��������߂�B����������߁C���������B

n��̎��s�Ŕԍ�n�̃J�[�h���R�̈�ԏ�ɗ���̂́C
�in�|1�j��̎��s�Ŕԍ��P�`n�|1�́in�|1�j���̃J�[�h��ԍ�n�̃J�[�h��艺�Ɏ����čs���C
���ƂP��̎��s�͔ԍ�n�̃J�[�h������ɒu���C�܂��͔ԍ�n�̃J�[�h���̂����̂܂�ɒu��
�E�E�E�E�E�E��
�Ƃ����ꍇ�ł���B
k���P��k��n�|1�̐����Ƃ���B
�i�A�j�@�ԍ�k�̃J�[�h������ԍ�n�̃J�[�h������ɒu���ꍇ
�@�ԍ�k�̃J�[�h��ԍ�n�̃J�[�h������ɒu�����@�́C
�@�@�@�@�@�@�in�|k�j�ʂ�B�@��k�̃J�[�h����n�̃J�[�h�܂łɒu���ꏊ���in�|k�j�ӏ�����̂ŁB
�@�in�|1�j���̃J�[�h��ԍ�n�̃J�[�h��艺�Ɏ����čs���ړ��̑����́C
�@�@�@�@�@�@�in�|1�j�I�ʂ�@���P��ڂ�k�̃J�[�h�̈ړ������āC�ォ�珇�ɌJ��o�����@���C�P�~�Q�~�R�~�E�E�E�~�in�|1�j�ʂ�B
�@������C�i�A�j�̏ꍇ�̐��́C�in�|k�j�~�in�|1�j�I�ʂ�
�@k�ɂP����n�|1�܂ő�����ĉ�����ƁC
�@�@�@�@�@�@�o1�{2�{3�{�E�E�E�{�in�|1�j�p�~�in�|1�j�I
�@�@�@�@�@![]()
�i�C�j�@�ԍ�n�̃J�[�h���̂����̂܂�ɒu���ꍇ
�@�ԍ��P�`n�|1�́in�|1�j���̃J�[�h��ԍ�n�̃J�[�h��艺�Ɏ����čs���ړ��̑��������߂āC
�@�@�@�@�@�@�in�|1�j�I�ʂ�@�������܂ŗ�����Ƃ͎�����邾���B
�i�A�j�C�i�C�j���C���̑����́C
�@�@�@�@![]()
���߂�m���́C
�@�@�@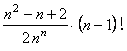
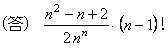
|
�@�S�D�@ �@�@�@���R��n�ɑ��ĕ��ʏ�̓_�on�ixn �Cyn�j�� �@�@�@�@�@�@�@�@ �@�@�ɂ���߂�B �@�@�����B�����łn�͌��_�ł���B |
[��]�@
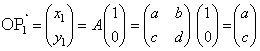
![]()

![]()
������ad�|bc��1�Ƈ@��p���āC�@�������ȒP�Ȃ��̂ɕό`���Ă����B
|
�ia2�{ad�|1�j2�{c2�ia�{d�j2��1 ���i�@�j�̒��̎�������������B { a�ia�{d�j�|1}2�|1�{c2�ia�{d�j2��0 a2�ia�{d�j2�|2a�ia�{d�j�{c2�ia�{d�j2��0 �ia2�{c2�j�ia�{d�j2�|2a�ia�{d�j��0 �ia�{d�j{�ia�{d�j�|2a }��0 �ia�{d �j�id�|a�j��0�@�@���ȒP�Ȏ��ɂȂ����B |
����āC�@�@a��d �@�܂��́@a���|d�@�����̂Q�̏ꍇ�ׂĂ����B
�i�@�j�@a��d �̂Ƃ�
�@ad�|bc��1��a2�|bc��1��1�|a2�{bc��0��c2�{bc��0��c�ib�{c�j��0�@���������������B
�@�@�@�@�@�@�@��c��0�܂���b�{c��0
�@�i�A�jc��0�̂Ƃ�
�@�@�@�ix1 �Cy1�j���ia �C0�j�C�ix2 �Cy2�j���ia2�C0�j�ƂȂ�B�@��y���ǂ���O�ɂȂ肻�����B
�@�@�@�ixn �Cyn�j���ian�C0�j�Ɖ��肷��C
�@�@�@�@�@�@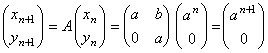
�@�@�@�ƂȂ�̂ŁC���ׂĂ�n�Łixn �Cyn�j���ian�C0�j�Ƃ�����B���A�[�@�B
�@�@�@�@���a2��1������Cxn2�{yn2���ian�j2���ia2�jn��1�@������Ŏ������B
�@�@�@
�@�i�C�jb�{c��0�̂Ƃ�
�@�@�@�@�@�@�@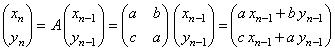 �@�@�@�@
�@�@�@�@
�@�@�@�@�@xn2�{yn2���ia xn�|1�{b yn�|1�j2�{�ic xn�|1�{a yn�|1�j2�@���Q���������B
���ia2�{c2�jxn�|12�{2
a�ib�{c�jxn�|1 yn�|1�{�ia2�{b2�jyn�|12
��xn�|12�{�oa2�{�i�|c�j2 } yn�|12
�@�@�@�@�@�@�@�@ ��xn�|12�{yn�|12�@
�@�@�@�@�@�@�@�@�@��xn�|22�{yn�|22���E�E�E��x12�{y12��a2�{c2��1�@���������������B
�@�i�A�j�C�i�C�j�̂ǂ���̏ꍇ���C���ׂĂ�n�ɑ��āC
�@�@�@�@�@�@�@�@![]()
�i�A�j�@a���|d �̂Ƃ�
�@�@ad�|bc��1��a2�{bc���|1������C
�@�@�@�@�@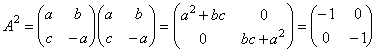
�@�@�@�@�@�@�@���n�~���g�����g���Ă��BA2�|(a�{d) A�{�iad�|bc) E��O��A2���|E�ƂȂ�B
�@�@�@�@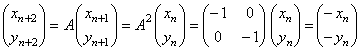
�@�@������C�@xn�{22�{yn�{22��xn2�{yn2�@
�@�@�E�@n����̂Ƃ��C�@xn2�{yn2��xn�|22�{yn�|22���E�E�E��x12�{y12��1�@�����������Ă����B
�@�E�@n�������̂Ƃ��C�@xn2�{yn2��xn�|22�{yn�|22���E�E�E��x22�{y22��1�@
�@�@����āC���ׂĂ�n�ɑ��āC
�@�@�@�@�@�@�@�@![]()
�i�@�j�C�i�A�j���C���ׂĂ�n�ɑ���![]() �̒����͂P�ł���B�@�@�@�@�@�@�@�@�@�@�i�ؖ��I���j
�̒����͂P�ł���B�@�@�@�@�@�@�@�@�@�@�i�ؖ��I���j
|
�@�T�D�@xy���ʏ�Ō��_���ɁCx���̐��̕������n���Ƃ���ɍ��W�Ɋւ��āC�ɕ����� �@�@�@r��2�{cos�� �i0���Ɓ��j�ɂ��\�����Ȑ���C�Ƃ���BC��x���Ƃň͂܂ꂽ�}�`��x�� �@�@�@�̂܂��ɂP��]���ē����闧�̂̑̐ς����߂�B |
[��]�@
�ɕ�����r��2�{cos�Ƃ����W�̔}��ϐ��\���ɒ����ƁC
�@�@�@x��r cos�Ɓ�cos��(2�{cos��)
y��r sin�Ɓ�sin��(2�{cos��)�@ �����Ƃ͌����ʂ�ɁB
![]()
![]()
y��0�̂Ƃ��C�Ɓ�0�C�@�ix�Cy�j���i3�C0�j�C�i�|1�C0�j ��x���Ƃ̌�_�B

�̐�V�́C
�@![]()
�@�@�@x�@�F�@�|1�@���@3�@
�@�@�Ɓ@�F�@�@�@���@0�@�@���ϕ����
������C
�@�@![]()
�@�@�@![]()
cos�Ɓ�t�Ƃ����ƁC�ƁF�@�@���@0�@�̂Ƃ��C t �F�@�|�P�@���@�P�@������C���u������B
�@�@�@![]()
�@�@�@�@![]()
�@�@�@�@![]()
�@�@�@�@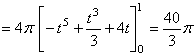
![]()
|
�@�U�D�@ a��b���݂��ɑf�C���Ȃ킿�P�ȊO�̌��������Ȃ����̐����Ƃ��C�����a�͊�� �@�@�@����B���̐���n�ɑ��Đ���a n�Cb n�� �@�@�@�@�@�@�@�@�@ �@�@�@���݂����悤�ɒ�߂�Ƃ��C���́i�P�j�C�i�Q�j�������B �@�@�@������ �@ �@�i�P�j�@a2�͊�ł���Ca2��b2�݂͌��ɑf�ł���B �@ �i�Q�j ���ׂĂ�n�ɑ��āCa n�͊�ł���Ca n��b n�݂͌��ɑf�ł���B |
[��]�@
�i�P�j�@n��1�C2�̂Ƃ��C
�@�@�@![]()
�@�@�@![]()
�@�����͂��ꂼ�ꐮ����![]() ��������������C
��������������C
�@�@�@�@�@�@a1��a�Cb1��b
�@�@�@a2��a2�{2b2�Cb2��2a b�@��������悭���ďؖ�����B
a�͊������a2����ŁC�܂�2b2�͋���������Ca2�{2b2�͊�ł���B����{�
�@����āCa2�͊�ł���B
�@���ɁCa2��b2�����ʂȑf����d�����Ƃ���B���w���@�Ŏ����B
�@a2���������Cd��3�ȏ�̊�ł���B
d��b2�̖C�܂�ab�̖őf��������Ca�܂���b�̖ł���B
�@�i�A�jd��a�̖ł���Ƃ��@���ʓ|�����ꍇ��������B
�@�@�@�@2b2��a2�|a2�̉E�ӂ�d�̔{���ɂȂ�C������b��d�̔{���ɂȂ�B
�@�i�C�jd��b�̖ł���Ƃ�
�@�@�@�@a2��a2�|2b2�̉E�ӂ�d�̔{���ɂȂ�C������a��d�̔{���ɂȂ�B
�i�A�j���i�C�j��a�Cb���Ƃ���d�̔{���ƂȂ�̂ŕs�����B
�@����āCa2��b2�݂͌��ɑf�ł���B�@�@�@�@�@�@�@�@�i�ؖ��I���j
�i�Q�j�@���ׂĂ�n�ɑ��āCa n�͊�ł���Ca n��b n�݂͌��ɑf�ł���B�E�E�E�E�E�E��
�@�@���C���w�I�A�[�@�ŏؖ�����B
�@�k�P�ln��1�̂Ƃ�
�@�@�@���炩�Ɂ��͐��藧�B
�@�k�Q�ln��k�̂Ƃ��������藧�Ɖ��肷��B
�@�@�@![]()
�@�@�@�@�@�@�@�@�@�@�@![]()
�@�@�@�@�@�@�@�@�@�@�@![]()
�@�@������C �@ak+1��a�Eak�{2b�Ebk�@�@�E�E�E�E�E�E�@
bk+1��b�Eak�{a�Ebk �@�@�E�E�E�E�E�E�A
������Ca�Eak�͊�C�܂�2b�Ebk�͋���������Ca�Eak�{2b�Ebk �͊�ł���B
�@�@����āCak+1�͊�ł���B
�@�@
�@�@���ɁCak+1��bk+1�����ʂȑf����d�����Ƃ��Ė������B���܂��w���@���g���B
�@�@ak+1���������Cd��3�ȏ�̊�ł���B
�@�@�@�~a�|�A�~2b���C��bk�������B�@�@
a�Eak+1�|2b�Ebk+1��(a2�|2b2�jak
�@�@�@�~b�|�A�~a ���C��ak�������B�@�@
b�Eak+1�|a�Ebk+1��(2b2�|a2�jbk
������̍��ӂ�d�̔{��������C�E�ӂ�d�̔{���ł���Ba2�|2b2��d�̔{���łȂ��Ƃ���ƁC
�@�@ak�Cbk���Ƃ���d�̔{���ƂȂ�݂��ɑf�łȂ��Ȃ�̂ŁCa2�|2b2��d�̔{���ł���B
�@�@
�@�@������b��d�̔{���Ȃ�Ca2���ia2�|2b2�j�{2b2�̉E�ӂ�d�̔{���ƂȂ�C����a��d�̔{���ƂȂ�B
�@�@a��b�݂͌��ɑf�����炱��͕s�����B�����b��d�̔{���ł͂Ȃ��B���@���̏����͂��ƂŎg���B
�@�@�@��ό`���āC
�@�@�@�@�@�@�@ak+1��a�ia�Eak�|1�{2b�Ebk�|1�j�{2b�Ebk�@��bk�@��d�̔{���ɂȂ邱�Ƃ��B
�@�@�@�@�@�@�@�@�@���ia2�|2b2�ja k�|1�{2b2 ak�|1�{2ab�Ebk�|1�{2b�Ebk
�@�@�@�@�@�@�@�@�@���ia2�|2b2�jak�|1�{2b�ib�Eak�|1�{a�Ebk�|1�j�{2b�Ebk
�@�@�@�@�@�@�@�@�@���ia2�|2b2�jak�|1�{4b�Ebk
�@������C4b�Ebk��ak+1�|�ia2�|2b2�jak�|1
�@�@����āC4b�Ebk��d�̔{���ł���C4b��d�̔{���ł͂Ȃ��̂ŁCbk��d�̔{���ƂȂ�B
�@�@�@���Ƃ��������ł��B
�@�@���̂Ƃ��A���Cb�Eak��bk+1�|a�Ebk�ŁC�E�ӂ�d�̔{���ƂȂ�C����ak��d�̔{���ƂȂ�B�@�@
�@�@�����ak�Cbk���Ƃ���d�̔{���ƂȂ�C�݂��ɑf�ł��邱�Ƃɖ�������B
�@�@�ȏ���Cak+1��bk+1�͋��ʂȑf�����������Ȃ��B
�@�@���Ȃ킿�Cak+1��bk+1�݂͌��ɑf�ł���̂ŁC����n��k�{�P�̂Ƃ������藧�B
�@����āC���ׂĂ�n�ɑ��ā��͐��藧�B�@�@�@�@�i�ؖ��I���j�@�@�I������E�E