200�X�N�@������w�i���ȁj�E�O���@���Ɖ�
�@
|
�@�P�D�@���W���ʂɂ����Č��_�𒆐S�Ƃ��锼�a2�̉~��C1�Ƃ��C�_�i1�C0�j�𒆐S�Ƃ��锼�a1�� �@�@�~��C2�Ƃ���B�܂��C�_(a�Cb)�𒆐S�Ƃ��锼�at�̉~C3���CC1�ɓ��ڂ��C����C2�ɊO�ڂ��� �@�@�Ɖ��肷��B�������Cb�͐��̎����Ƃ���B �@�@(1)�@ a�Cb��t��p���ĕ\���B�܂��Ct���Ƃ蓾��l�͈̔͂����߂�B �@�@(2)�@ t��(1)�ŋ��߂��͈͂��Ƃ��Cb�̍ő�l�����߂�B |
[��]�@
(1)�@
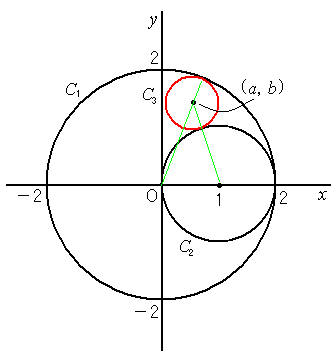
�@�~C3��C1�ɓ��ڂ���̂ŁC�����S�Ԃ̋����͔��a�̍��ɓ�����
�@�@�@�@�@�@![]()
�@�@�@�@�@a2�{b2���i t�|2�j2�@�E�E�E�E�E�E�i�A�j
�@�܂��C�~C3��C2�ɊO�ڂ���̂ŁC�����S�Ԃ̋����͔��a�̘a�ɓ�����
�@�@�@�@�@![]()
�@�@�@�@�i a �|1 �j2�{b2���it�{1�j2�@�E�E�E�E�E�E�i�C�j
�@�i�A�j�|�i�C�j���C�����Ƃ͘A�������������������B
�@�@�@�@�@a2�|�ia �|1�j2���it�|2�j2�|�it�{1�j2
�@�@�@�@�@�@�@�@�@�@�@2 a �|1���|6 t�{3
a ���|3 t�{2�@
�@�i�A�j���C�@b2���it�|2�j2�|a2
�@�@�@�@�@�@�@�@�@���i t�|2�j2�|�i�|3 t�{2�j2
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���|8 t 2�{8 t
�@![]()
�@b�����݂�������́C�|8 t 2�{8 t��0�@���Ȃ킿�C0��t��1
���̂Ƃ��C�~C3�͊m���ɑ��݂���B
![]()
(2)�@ 0��t��1�̂Ƃ��C�@t��0�C1�|t��0������C���i���敽�ρj���i�������ρj���g���B
�@�@![]()
�@![]()
�@![]()
|
�@�Q�D�@���R��m��2�ɑ��Cm�|1�̓W�� �@�@�@�@�@�@�@�@�@�@m�b1�@�C�@m�b2�@�C
�E�E�E �C m�bm�|1 ���l���C����炷�ׂĂ̍ő����dm�Ƃ���B���Ȃ킿�Cdm�͂���炷�ׂĂ������ő� �@�@�̎��R���ł���B �@�@(1)�@ m���f���Ȃ�Cdm��m�ł��邱�Ƃ������B �@�@(2)�@���ׂĂ̎��R��k�ɑ��Ckm�|k��dm�Ŋ����邱�Ƃ��Ck�Ɋւ��鐔�w�I�A�[�@�� �@�@�@����Ď����B �@�@�@�@�@�@ |
[��]�@
(1)�@�܂��C dm��m�b1�̖�����Cdm��m�@�E�E�E�@�@��dm��m�ȉ��ƂȂ邱�Ƃ��킩��B
�@���� r��1�C2�C�E�E�E�Cm�|1�Ƃ���B���W�����܂Ƃ߂čl���鏀���B
�@�@�@�@�@![]()
�@�@�@�����m�̂��̂���r�Ƃ����g�����̐���\���̂Ő����ł���B
�@�@�@���������ĕ��q�͕���̔{���ł��邪�Cm�͑f�������番��̂ǂ̈����Ƃ��݂��ɑf�ł���B
�@�@�@![]()
�@�@�@���Ȃ킿�Cm�br��m�̔{���ł���C����ɂ��Cdm��m�̔{���ƂȂ�B�@�E�E�E�A
�@�@�@�@�C�A���Cdm��m�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�ؖ��I���j
(2)�@ �u���ׂĂ̎��R��k�ɑ��Ckm�|k��dm�Ŋ�����v�E�E�E��
�@����𐔊w�I�A�[�@�ŏؖ�����B
�@(�@) k��1�̂Ƃ�
�@�@km�|k��0������C����͎��R��dm�Ŋ�����B����āC���͐��藧�B
�@(�A) k��p (p�͂��鎩�R��)�̂Ƃ��C�������藧�Ɖ��肷��B
�@�@�ip�{1)m�|�ip�{1)�� m�b0�{p�Em�b1�{p2�Em�b2�{�E�E�E�{pm�|1�Em�bm�|1�{pm�Em�bm�|�ip�{1) ���藝�œW�J�B
��p�Em�b1�{p2�Em�b2�{�E�E�E�{pm�|1�Em�bm�|1�{�i pm�|p )
�@�@�����ŁCm�b1�Cm�b2�C�E�E�E�Cm�bm�|1�͂��ׂ�dm�Ŋ����Cpm�|p�͋A�[�@�̉��肩��dm�Ŋ�����
�@�@�̂ŁC�ip�{1)m�|�ip�{1)��dm�Ŋ�����B
�@�@����āCk��p�{1�̂Ƃ����������藧�B
�@(�@)�C(�A)���C���͐��藧�B�@�@�@�@�@�@�@�@�@�@�@�@�i�ؖ��I���j
|
�@�R�D�@�X�C�b�`��1�����ƂɁC�ԁC�C���C���̂����ꂩ�̐F�̋ʂ�1�C���m���P�^�S�� �@�@�@�o�Ă���@�B������B�Q�̔��k�Ƃq��p�ӂ���B���̂R��ނ̑�����l����B �@�@�@�@�i�`�j�@�P��X�C�b�`�������C�o�Ă����ʂ��k�ɓ����B �@�@�@�@�i�a�j�@�P��X�C�b�`�������C�o�Ă����ʂ��q�ɓ����B �@�@�@�@�i�b�j�@�P��X�C�b�`�������C�o�Ă����ʂƓ����F�̋ʂ��C�k�ɂȂ�����̋ʂ��k�ɓ���C �@�@�@�@�@�@�k�ɂ�����̋ʂ��q�ɓ����B �@(1)�@�k�Ƃq�͋�ł���Ƃ���B����i�`�j��5���Ȃ��C����ɑ���i�a�j��5���Ȃ��B���̂Ƃ� �@�@�@�k�ɂ��q�ɂ�4�F���ׂĂ̋ʂ������Ă���m���o1�����߂�B �@(2) �k�Ƃq�͋�ł���Ƃ���B����i�b�j��5���Ȃ��B���̂Ƃ��C�k��4�F���ׂĂ̋ʂ������� �@�@�@����m���o2�����߂�B �@(3)�@ �k�Ƃq�͋�ł���Ƃ���B����i�b�j��10���Ȃ��B���̂Ƃ��k�ɂ��q�ɂ�4�F���ׂĂ̋ʂ� �@�@�@ |
[��]�@
(1)�@ �k��4�F���ׂĂ̋ʂ������Ă���̂́C�T��̐F�̏o����
�@�@�@�@�@�@�@�@���C�C���C���C��
�@�@�̂悤�ɂP�F���Q��C���̐F���P�o��ꍇ�ł���B���̂悤�ȐF�̏o���́C
�@�@�@�@�@�@�@�@5�b2�~4�I�ʂ�@���i�Q��o��F�̏ꏊ�j�~�i�F�̏��ԁj
�@�@����āC�k��4�F���ׂĂ̋ʂ������Ă���m���́C
�@�@�@�@�@�@�@�@![]()
�@�@�q��4�F���ׂĂ̋ʂ������Ă���m���������ł���B
�@�@�@�@�@�@�@![]()
�@![]()
(2)
����i�b�j��5���Ȃ����Ƃ��C�k��4�F���ׂĂ̋ʂ������Ă���̂́C
�@�@����i�`�j��5���Ȃ����Ƃ��C�k��4�F���ׂĂ̋ʂ����邱�ƂƓ����ł���B���i�P�j�ŋ��߂��B
�@![]()
(3)�@ ����i�b�j��10���Ȃ����Ƃ��C�k�ɂ��q�ɂ�4�F���ׂĂ̋ʂ������Ă���̂́C
�@�i�@�j�P�̐F���S��C���̐F���Q�o��
�@�i�A�j�Q�̐F���R��C���̐F���Q�o��@
�@���̂����ꂩ�ł���B�����ꂼ��̊m�������߂đ��������B
�@�i�@�j�̏ꍇ�̐F�̏o���́C���i�S��o��F�̑I���j�~�i�p�^�[���j
�@�@�@�@![]()
�@�@������C�m���́C
�@�@�@�@�@�@![]()
�@ �i�A�j�̏ꍇ�̐F�̏o���́C���i�R��o��F�̑I���j�~�i�p�^�[���j
�@�@�@�@�@![]()
�@�@������C�m���́C
�@�@�@�@�@�@![]()
�@����āC
�@�@�@�@�@�@![]()
�@�@�@�@�@�@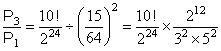
�@�@�@�@�@�@�@�@![]()
�@![]()
|
�@�S�D�@2���ȉ��̐���f (x)��ax 2�{bx�{c�ɑ��C �@�@�@�@ �@���l����B �@(1)�@ f ( 0 )��0�Cf ( 2 )��2�̂Ƃ���S��a�̊��Ƃ��ĕ\���B �@(2)�@ f ( 0 )��0�Cf ( 2 )��2���݂����Ȃ���f���ω�����Ƃ��CS�̍ŏ��l�����߂�B |
[��]�@
(1)�@ f ( 0 )��0���Cc��0
�@�@�@f ( 2 )��2���C4a�{2b��2�@�@b��1�|2 a
����āC�@f �L( x )��2ax�{�i1�|2 a �j
�@ a��0�̂Ƃ��Cf �L( x )��1������C
�@�@�@�@�@![]()
�@�@�ȉ��Ca��0�̂Ƃ����l����B
�@�@�@�@f �L( x )��0�ƂȂ�l��t�Ƃ���ƁC2at�|�i2 a�|1�j��0�@���L�q���₷���悤�ɒu�������Ă���
![]()
�܂��C�@f �L( 0 )��1�|2 a�C f �L( 2 )��2 a�{1�@���ϕ���ʐςŋ��߂�̂ŁC���̒l���K�v�B
�@�@
�@�i�@�j�@t��0�C2��t�̂Ƃ��@���܂���̋�����Ԃ̊O�ɂ���ꍇ
�@�@�@�@�@�@![]()
�@�@�@�@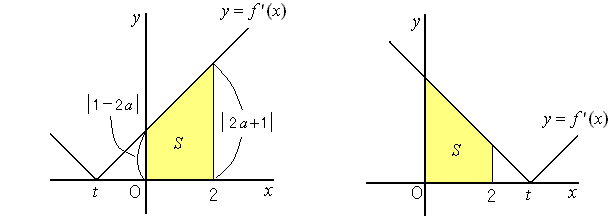
�@�@�@�@![]()
�@�@�@�@�@���i1�|2 a�j�{�i2 a�{1�j��2�@���萔�ɂȂ�܂����B
�i�A�j�@0��t��2�̂Ƃ��@���܂���̋�����Ԃ̒��ɂ���ꍇ
�@�@�@�@�@�@![]()
�@�@�@�@�@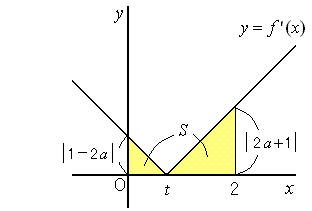
�@�@�@�@![]()
�@�@�@�@�@![]() �@����Βl���P�ɂ܂Ƃ߂�ƁC���ꂢ�Ȏ��ɂȂ�B
�@����Βl���P�ɂ܂Ƃ߂�ƁC���ꂢ�Ȏ��ɂȂ�B
�@�@�@�@�@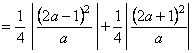 �@�@
�@�@
�@�@�@�@�@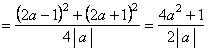 �@�@���Q��́C��Βl���͂�����B
�@�@���Q��́C��Βl���͂�����B
�@![]()
�@�@�@�@![]()
![]()
�@�@�@�@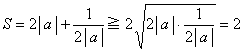 �@���i�������ρj���i���敽�ρj
�@���i�������ρj���i���敽�ρj
�@![]()
�@![]()
�@![]()