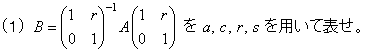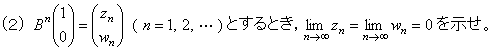200�X�N�@������w�i���ȁj�E�O���@���Ɖ�
�@
|
�@�P�D�@���R��m��2�ɑ��Cm�|1�̓W�� �@�@�@�@�@�@�@�@�@�@m�b1�@�C�@m�b2�@�C
�E�E�E �C m�bm�|1 ���l���C����炷�ׂĂ̍ő����dm�Ƃ���B���Ȃ킿�Cdm�͂���炷�ׂĂ������ő� �@�@�̎��R���ł���B �@�@(1)�@ m���f���Ȃ�Cdm��m�ł��邱�Ƃ������B �@�@(2)�@���ׂĂ̎��R��k�ɑ��Ckm�|k��dm�Ŋ����邱�Ƃ��Ck�Ɋւ��鐔�w�I�A�[�@�� �@�@�@����Ď����B �@�@(3)�@ m�������̂Ƃ�dm��1�܂���2�ł��邱�Ƃ������B �@�@�@�@�@�@ |
[��]�@
(1)�@�܂��C dm��m�b1�̖�����Cdm��m�@�E�E�E�@�@��dm��m�ȉ��ƂȂ邱�Ƃ��킩��B
�@���� r��1�C2�C�E�E�E�Cm�|1�Ƃ���B���W�����܂Ƃ߂čl���鏀���B
�@�@�@�@�@![]()
�@�@�@�����m�̂��̂���r�Ƃ����g�����̐���\���̂Ő����ł���B
�@�@�@���������ĕ��q�͕���̔{���ł��邪�Cm�͑f�������番��̂ǂ̈����Ƃ��݂��ɑf�ł���B
�@�@�@![]()
�@�@�@���Ȃ킿�Cm�br��m�̔{���ł���C����ɂ��Cdm��m�̔{���ƂȂ�B�@�E�E�E�A
�@�@�@�@�C�A���Cdm��m�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�ؖ��I���j
(2)�@ �u���ׂĂ̎��R��k�ɑ��Ckm�|k��dm�Ŋ�����v�E�E�E��
�@����𐔊w�I�A�[�@�ŏؖ�����B
�@(�@) k��1�̂Ƃ�
�@�@km�|k��0������C����͎��R��dm�Ŋ�����B����āC���͐��藧�B
�@(�A) k��p ( p�͂��鎩�R��)�̂Ƃ��C�������藧�Ɖ��肷��B
�@�@�ip�{1)m�|�ip�{1)�� m�b0�{p�Em�b1�{p2�Em�b2�{�E�E�E�{pm�|1�Em�bm�|1�{pm�Em�bm�|�ip�{1) ���藝�œW�J�B
��p�Em�b1�{p2�Em�b2�{�E�E�E�{pm�|1�Em�bm�|1�{�i pm�|p )
�@�@�����ŁCm�b1�Cm�b2�C�E�E�E�Cm�bm�|1�͂��ׂ�dm�Ŋ����Cpm�|p�͋A�[�@�̉��肩��dm�Ŋ�����
�@�@�̂ŁC�ip�{1)m�|�ip�{1)��dm�Ŋ�����B
�@�@����āCk��p�{1�̂Ƃ����������藧�B
�@(�@)�C(�A)���C���͐��藧�B�@�@�@�@�@�@�@�@�@�@�@�@�i�ؖ��I���j
(3)�@ m��2�̂Ƃ��C(1)���C�@dm��2
�@�@m��4�̂Ƃ��C�@�@4�b1��4�b3��4�C�@4�b2��6�@�̍ő����2������Cdm��2
�@�@m��6�̂Ƃ��C�@�@6�b1��6�b5��6�C�@6�b2��6�b4��15�C6�b3��20�@�̍ő����1������Cdm��1
�@�@�ȏ��dm�͂P�ƂQ�̒l���Ƃ蓾�邱�Ƃ��킩�����B���Ƃ͂���ȊO�̒l���Ƃ�Ȃ����Ƃ����������B
�@m��8�ȏ�̋����̂Ƃ����l����B
�@�@T (k)��km�|k�Ƃ���B(2)���Cdm�͂��ׂĂ�T (k)�̌��ł���B
�@�@�����ŁCp��3�ȏ�̐����Ƃ���ƁC
�@ �@ T ( p�|1)��(p�|1)m�|( p�|1) ����J���Ĕ��������E�E�B
��pm�|pm�|1�{pm�|2�|�E�E�E�{(�|1) r p m�|r�{�E�E�E�{(�|1) m�|1p�{(�|1) m�|p�{1
��p{ pm�|1�|pm�|2�{�E�E�E�{(�|1) r p m�|r�|1�{�E�E�E�{(�|1) m�|1�|1}�{(�|1) m�{1
�@�@�@�@
��p { pm�|1�|pm�|2�{�E�E�E�{(�|1) r p m�|r�|1�{�E�E�E�{(�|1) m�|1�|1}�{2�@ ��m�͋���������B
�@�@����āCT ( p�|1)��p�Ŋ������Ƃ��̗]���2�ƂȂ�CT ( p�|1)��p�Ŋ����Ȃ��B
�@�@���̂��Ƃ���C���ׂĂ�T (k)�̌��ɁC3�ȏ�̐����͂Ȃ����Ƃ��킩��B
�@�@�ȏ���Cm�������̂Ƃ��Cdm��1�܂���dm��2�ł���B�@�@�@�i�ؖ��I���j
|
�@�Q�D�@�����𐬕��ɂ��s�� �@�@�@�@�@�@�@�@�@�@�@ �@�@�Ǝ���r�Cs�����̏���(�@)�C(�A)�C(�B)���݂����Ƃ���B �@�@ �@�@(�@) s��1 ���̂Ƃ��ȉ��̖�ɓ�����B �@ �@ �@(3)�@ c��0 ���� | a |��1�������B |
[��]�@
![]()
�@�@�@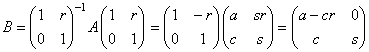
�@![]()
![]()
�@�@B��T -1AT�̗��ӂ�n�悷��ƁC ������͂悭����`�B
�@�@�@�@�@�@�@�@Bn ���iT -1AT�jn
�@�@�@�@�@�@�@�@�@�@��T -1AT �ET -1AT �ET -1AT �E�E�E�E T -1AT
��T -1AEAEAE �E�E�E�E AEAT
�@�@�@�@�@�@��T -1AAA�E�E�E�EAT
��T -1A n
T�@��������g����z��w�����߂�B
�@�@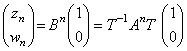
�@�@�@�@�@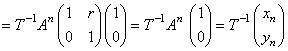
�@�@�@�@�@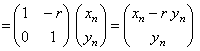
�@�@�@�@�@�@�@�@�@�@�@�@�@���܂��s���������B
�@�@![]()
�@�@�@�@�@�@�@�@![]()
�@�@�@�@�@�@�@�@![]()
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�ؖ��I���j
(3)�@�܂��@Bn �����߂�Ba�|cr��t �Ƃ����ƁC�@�����₷���悤�ɒu��������
�@�@�@![]()
�@
�@������C���E�オ�O�̍s��͐������₷���B
�@�@�@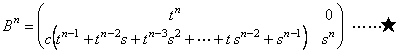
�@�Ɛ����ł���B����𐔊w�I�A�[�@�ŏؖ�����B�����Ăɂ͏����Ă��������������ł��傤�B
�@�i�A�j�@n��1�̂Ƃ��C���͐��藧�B
�@�i�C�j�@n��k �̂Ƃ��C�������藧�Ɖ��肷��ƁC
�@�@�@�@�@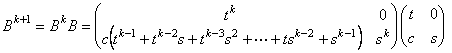
�@�@�@�@�@�@�@�@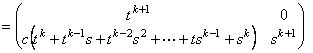
�@�@�@�ƂȂ�̂ŁCn��k�{1�̂Ƃ����������藧�B
�@�i�A�j�C�i�C�j���C���͐������B
�@�@�@�@����ŁCz��w���v�Z�ł���悤�ɂȂ����B
�@�@�@�@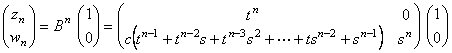
�@�@�@�@�@�@�@�@
�@![]()
�@s��1������Cs�|t��0�ł���B�����ŁC
�@�@�@�@![]()
�@������Cc��0�Ƃ���C���w���@�̂悤�Ȏ������B
�@�@�@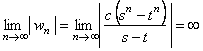
�@�ƂȂ�C(2)�̌��ʂɖ�������B����āC c��0
�@���̂Ƃ��C| t |��| a�|cr |��| a |�C | t |��1 ������C| a |��1
�i�ؖ��I���j
|
�@�R�D�@�X�C�b�`��1�����ƂɁC�ԁC�C���C���̂����ꂩ�̐F�̋ʂ�1�C���m��1/4�� �@�@�@�o�Ă���@�B������B�Q�̔��k�Ƃq��p�ӂ���B���̂R��ނ̑�����l����B �@�@�@�@�i�`�j�@�P��X�C�b�`�������C�o�Ă����ʂ��k�ɓ����B �@�@�@�@�i�a�j�@�P��X�C�b�`�������C�o�Ă����ʂ��q�ɓ����B �@�@�@�@�i�b�j�@�P��X�C�b�`�������C�o�Ă����ʂƓ����F�̋ʂ��C�k�ɂȂ�����̋ʂ��k�ɓ���C �@�@�@�@�@�@�k�ɂ�����̋ʂ��q�ɓ����B �@(1)�@�k�Ƃq�͋�ł���Ƃ���B����i�`�j��5���Ȃ��C����ɑ���i�a�j��5���Ȃ��B���̂Ƃ� �@�@�@�k�ɂ��q�ɂ�4�F���ׂĂ̋ʂ������Ă���m���o1�����߂�B �@(2) �k�Ƃq�͋�ł���Ƃ���B����i�b�j��5���Ȃ��B���̂Ƃ��C�k��4�F���ׂĂ̋ʂ������� �@�@�@����m���o2�����߂�B �@(3)�@ �k�Ƃq�͋�ł���Ƃ���B����i�b�j��10���Ȃ��B���̂Ƃ��k�ɂ��q�ɂ�4�F���ׂĂ̋ʂ� �@�@�@ |
[��]�@
(1)�@ �k��4�F���ׂĂ̋ʂ������Ă���̂́C�T��̐F�̏o����
�@�@�@�@�@�@�@�@���C�C���C���C��
�@�@�̂悤�ɂP�F���Q��C���̐F���P�o��ꍇ�ł���B���̂悤�ȐF�̏o���́C
�@�@�@�@�@�@�@�@5�b2�~4�I�ʂ�@���i�Q��o��F�̏ꏊ�j�~�i�F�̏��ԁj
�@�@����āC�k��4�F���ׂĂ̋ʂ������Ă���m���́C
�@�@�@�@�@�@�@�@![]()
�@�@�q��4�F���ׂĂ̋ʂ������Ă���m���������ł���B
�@�@�@�@�@�@�@![]()
�@![]()
(2)
����i�b�j��5���Ȃ����Ƃ��C�k��4�F���ׂĂ̋ʂ������Ă���̂́C
�@�@����i�`�j��5���Ȃ����Ƃ��C�k��4�F���ׂĂ̋ʂ����邱�ƂƓ����ł���B���i�P�j�ŋ��߂��B
�@![]()
(3)�@ ����i�b�j��10���Ȃ����Ƃ��C�k�ɂ��q�ɂ�4�F���ׂĂ̋ʂ������Ă���̂́C
�@�i�@�j�P�̐F���S��C���̐F���Q�o��
�@�i�A�j�Q�̐F���R��C���̐F���Q�o��@
�@���̂����ꂩ�ł���B�����ꂼ��̊m�������߂đ��������B
�@�i�@�j�̏ꍇ�̐F�̏o���́C���i�S��o��F�̑I���j�~�i�p�^�[���j
�@�@�@�@![]()
�@�@������C�m���́C
�@�@�@�@�@�@![]()
�@ �i�A�j�̏ꍇ�̐F�̏o���́C���i�R��o��F�̑I���j�~�i�p�^�[���j
�@�@�@�@�@![]()
�@�@������C�m���́C
�@�@�@�@�@�@![]()
�@����āC
�@�@�@�@�@�@![]()
�@�@�@�@�@�@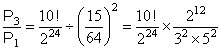
�@�@�@�@�@�@�@�@![]()
�@![]()
|
�@�S�D�@a�𐳂̎����Ƃ��C��ԓ���2�̉~�� �@�@�@�@�@�@�@D1���o ( x�Cy�Cz ) | x 2�{y2��1�Cz��a �p �@�@�@�@�@�@�@D2���o ( x�Cy�Cz ) | x 2�{y2��1�Cz���|a �p �@���l����BD1��y���̉���180����]����D2�ɏd�˂�B��������]��z���̐��̕�����x���� �@���̕����ɌX��������Ƃ���B���̉�]�̊Ԃ�D1���ʂ镔����E�Ƃ���BE�̑̐ς�V ( a )�Ƃ��C �@E�Ɓo ( x�Cy�Cz ) | x��0�p�Ƃ̋��ʕ����̑̐ς�W ( a )�Ƃ���B �@(1)�@ W ( a )�����߂�B �@ �@ |
[��]�@
(1)�@ E���l����ɂ́C���̗��̂�y��t�Ő�������̐}�`�̖ʐς��l����B

�@y��t�Ő�������̂���x��0�̕����̖ʐς́C�����~���甼�~��蔲�����`�ɂȂ�B
�@�@�@�@![]()
�@����āC���Ƃ͐ϕ���������B
�@�@�@�@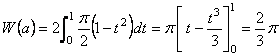
�@![]()
(2)�@y��t�Ő�������̂���x��0�̕����̖ʐς�S ( t ) �Ƃ���B������S ( t )�����߂�̂͑�ρB
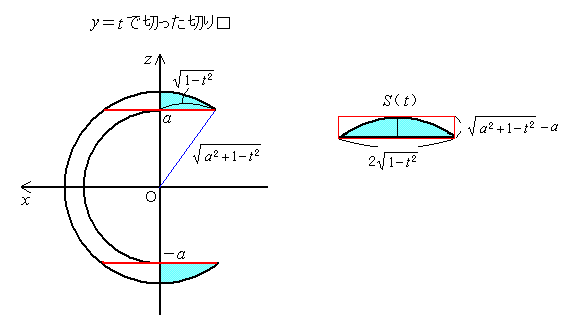
�@�@S ( t ) ����}�̒����`�̖ʐςƔ�r����ƁC�@���s�����ł͂��ށB���̖�ł́C����ȑ�G�c�ȍ��ł��܂��s���B
�@�@�@�@![]()
�@�����ŁC�@���܂��ϕ����Ȃ��B�E�ӂ������ƊȒP�Ȏ��ɂ���B
�@�@�@�@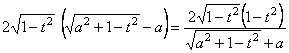
�@![]()
�@������C
�@�@�@�@�@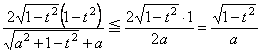
�@![]()
�@�@�@�@�@�@�@�@�@���ϕ������l���O�Ɏ������������C�Ƃ����\�������Ƃɂ��̕s�������������B
�@E�Ɓo ( x�Cy�Cz ) | x��0�p�Ƃ̋��ʕ����̑̐ς�X ( a )�Ƃ���ƁCV ( a )��W ( a )�{X ( a )
![]()
![]()
![]()
�@![]()
![]()
![]() �@
�@
|
�@�T�D�@(1)�@����x���|1��x��1�Cx��0���݂����Ƃ��C���̕s�����������B �@�@�@�@�@�@�@�@�@�@ �@�@(2)�@���̕s�����������B
0.9999101��0.99��0.9999100 |
[��]�@
(1)�@ �|1��x��1������C1�|x��0�C1�{x��0�@�܂��Cx2��0
�@�@�@![]() �Ɠ��l�ȕs����������B
�Ɠ��l�ȕs����������B
�@�@�@![]()
�@�@�@�@�@�@�@�@�@�@�@�@
�@![]()
![]()
����āC�����ؖ�����B�����������̂���錾���Ă����B
�@![]() �@���O����x�͖������āB
�@���O����x�͖������āB
�@�Ƃ����ƁCx��0�̂Ƃ�y��0�@���̒l���܂߂čl����B
�@�@�@![]()
�@�@�@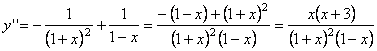
�@����āC�@�|1��x��0�̂Ƃ��Cy''��0������Cy' �͒P�������B�@�@
0��x��1�̂Ƃ��C y''��0������Cy' �͒P�������B
�@x��0�̂Ƃ� y'��0�@������C�@
�@�@�@�@�@�@�|1��x��0�̂Ƃ��Cy'��0
�@�@�@�@�@�@0��x��1�̂Ƃ��C
y'��0�@�ƂȂ�B���ǂ�������ɂȂ����B
�@����āC�|1��x��1�̂Ƃ�y�͒P�������ł���̂ŁC
�@�@�@�@�@�@�|1��x��0�̂Ƃ��Cy��0
�@�@�@�@�@�@0��x��1�̂Ƃ��C
y��0�@
�@�ȏ���C�|1��x��0�̂Ƃ��Cx y��0
�@�@�@�@�@�@�@0��x��1�̂Ƃ��C
x y��0
�@��������̂ŁC���͐��藧�B�@�@�@�@�@�@�@�@�@�@�@�@�i�ؖ��I���j
(2) �@(1)�̕s������ό`����B
�@�@�@�@1�|x��0.99�Ƃ݂��x��0.01�ŁC0.9999��1�|x2�ɂȂ�B��������z���Ď��ό`���l����B
�@�@![]()
�@�@�@�@�@![]()
�@�@�@�@�@�@![]()
�@���̎���x��0.01��������ƁC0.99��0.9999100�@�@�E�E�E�E�E�E�i�A�j
�@![]() �@
�@
�@�@�@�@�@![]()
�@�@�@�@�@![]()
�@���̎���x���|0.01��������ƁC0.9999101��0.99�@�@�E�E�E�E�E�E�i�C�j
�@�i�A�j�C�i�C�j���C0.9999101��0.99��0.9999100�@�@�@�@�@�@�@�i�ؖ��I���j
|
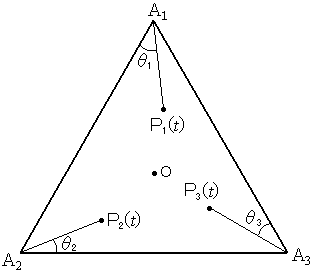
�@�U�D�@���ʏ�̂Q�_�o�C�p�̋�����d�i�o�C�p�j�ƕ\�����Ƃɂ���B���ʏ�ɓ_�n�𒆐S�Ƃ����ӂ� �@�@�@������1000�̐��O�p�`���`1�`2�`3������B���`1�`2�`3�̓����ɂR�_�a1�C�a2�C�a3���C d�i�`n �C�an �j��1 �in��1�C2�C3�j�@�ƂȂ�悤�ɂƂ�B�܂��C �@�@�@�@�@�@�@�@
�@�@�Ƃ����Bn��1�C2�C3�̂��ꂼ��ɑ��āC����0�ɂ`n���o�����C �@�@�_���l���C����t�ɂ����邻�̈ʒu���on�it�j�ƕ\�����Ƃɂ���B �@(1)�@���鎞��t��d�i�o1�it�j�C�o2�it�j�j��1�����������B�x�N�g�� �@�@�@�ƂƂ����B���̂Ƃ� �@(2)�@�p�x��1�C��2�C��3����1���ڂa1�`1�`2�C��2���ڂa2�`2�`3�C��3���ڂa3�`3�`1�ɂ���Ē�`����B �@�@�@���� �@�@�@�Ƃ�͈͂�����p���ĕ\���B �@(3)�@����t1�Ct�Q�Ct�R �̂��ꂼ��ɂ����āC�������������B �@�@�@�@�@�@d�i�o2�it1�j�C�o3�it1�j�j��1�C d�i�o3�it�Q�j�C�o1�it�Q�j�j��1�C d�i�o1�it�R�j�C�o3�it�R �j�j��1 ���̂Ƃ��C���� �@�@�@�@�@�@d�i�o1�iT�j�CO�j��3�C d�i�o2�iT�j�CO�j��3�C d�i�o3�iT�j�CO�j��3 �@�@�@���������邱�Ƃ������B |
[��]�@
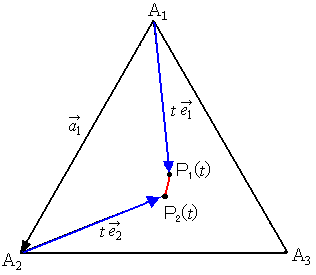
(1)�@ �Ƃ肠�����}�����Ă݂�B
�@�@
�@
�@�@�o1�it�j���o1�C�o2�it�j���o2�ƕ\���ƁC�o1�o2���P�@��������x�N�g���ŕ\�����B
�@�@![]()
�@�@![]()
�@�@![]()
�@�@�_�`2���璼���`1�p�ɐ����`2�g���Ђ��ƁC�`2�g���`2�p��1�@������ōs�������B
�@�@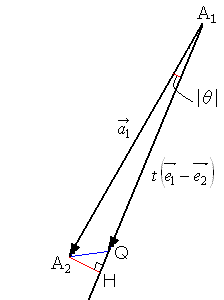
�@�@�`2�g��1000|sin��| ������C1000|sin��|��1
�@�@![]()
�@�@
(2)
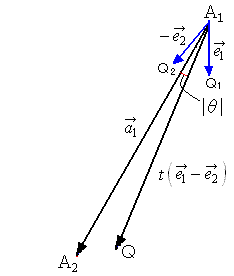
�@(1)�̕s�������݂����Ƃ͈̔͂́C�|�����Ɓ����@�E�E�E�i�A�j�@������𗘗p������j�B
�@�@�@![]()
�@�@�@�`1Q1���`1Q2������C�`1�p�́ڂp1�`1
Q2�̓����ł���B
�@�@
�@�@![]()
�@�@![]()
�@�@�@�@�@�@�@�@![]()
�@�@�i�A�j���C
�@�@�@�@�@�@�@![]()
�@�@�@�@�@�@�@�@�@![]()
�@�@![]()
(3)�@(2)�Ŏ������s�����Ɠ��l�ɁC�������藧�B
�@�@�@�@![]() �@
�@
�@�@�@�@![]()
�@�@(2)�̕s�����Ɓi�E�j��ӁX�����āC
�@�@�@�@![]()
�@�@![]()
�@�@������ӁX������2�Ŋ���ƁC����2�C��3�������B
�@�@�@�@![]() �@
�@
�@�@��2�C��3�͈̔͂������ł���B
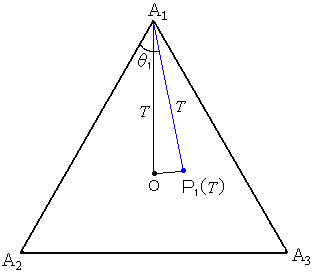
�@�@���ɁC���`1�n�o1�iT�j���l����B���]���藝���g���Ăn�o1�iT�j�����߂�B
�@�@�@�@�@![]()
�@�@�@�@
![]()
![]()
�@�@������C�@�@
�@�@�@�@�@�@d�i�o1�iT�j�CO�j��3�@�� {�n�o1�iT�j}2��9�@�������ׂ��s����������������B
![]()
![]()
�@�@d�i�o2�iT�j�CO�j��3�C d�i�o3�iT�j�CO�j��3�ɂ��ẮC���̃�1�����ꂼ���2�C��3�ɓ���ւ����s�����Ɠ��l�ł���B
�@�@����āi�G�j�̏����̂��ƂŁ��������C�ؖ����ׂ��R�̕s���������藧���Ƃ�������B
�@�@![]()
�@�@![]()
�@�@�����ŁCcos3�������߂�Bsin����s�Ƃ���ƁC��cos3�������̉E�ӂ��傫�����Ƃ����������B
�@�@�@�@�@�@�@�@�@![]()
�@�@�@�@�@cos3����4cos3���|3cos��
|
|
��cos���i4cos�Q���|3�j ��cos���o4�i1�|s2�j�|3�p ��cos���i1�|4s2�j�@ ��cos2���i1�|4s2�j���i1�|s2�j�i1�|4s2�j�@��cos����cos2�����g���B ��1�|5s2�{4s�S ��4 s 4�@�͖�������B ��1�|5s2 �����̉E�ӂɋ߂Â��Ă����B
|
�@�@����āC�������藧�B�@�@�@�@�@�@�@�i�ؖ��I���j