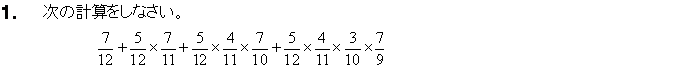200�V�N�@���{�W���j�A���w�I�����s�b�N�@���Ɖ�
�@
2007�N1��8���@��������2����
|
�@ |
[��]

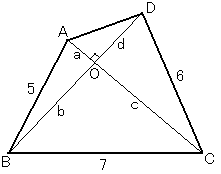
�@�Q�D�@�@�l�p�`ABCD�ɂ�����AB��5�CBC��7�CCD��6�ł���C�Ίp��AC��BD�͎l�p�`�̓��� �@�@�Œ������Ă���BDA�����߂�B |
[�l����]�@
������ꂽ�S�̎O�p�`�ŎO�����̒藝���g���܂��B
�@�@
[��]
|
OA��a�COB��b�COC��c�COD��d�Ƃ���B �O�����̒藝����C ��OAB�ŁC�@a2�{b2��25�@�E�E�E�E�E�E�@ ��OBC�ŁC�@b2�{c2��49�@�E�E�E�E�E�E�A ��OCD�ŁC�@c2�{d2��36�@�E�E�E�E�E�E�B �@�{�B�|�A���C�@ a2�{d2��12�@��DA�̂Q��̎������܂� �@�@�@DA2��12 |
|
![]()
|
�@ |
[�l����]�@
����ƕ��q�����ꂼ�ꕶ���ł����āC�ʕ����C���Ă͂܂镪�q�̐����l���܂��B
[��]

|
�@�S�D�@�@�������W���Ƃ���R���̂R�ϐ�������f ( x�Cy�Cz ) �ł����āC���̏����������̂��P�� �@�@�@���߂�B �@�@�@�@�@�E�@f ( x�Cy�Cz )�{x��y�{z�Ŋ�����B �@�@�@�@�@�E�@f ( x�Cy�Cz )�{y��z�{x�Ŋ�����B �@�@�@�@�@�E�@f ( x�Cy�Cz )�{z��x�{y�Ŋ�����B �������C������P ( x�Cy�Cz ) ��������Q ( x�Cy�Cz ) �Ŋ�����Ƃ́C �@�@�@P ( x�Cy�Cz )��Q ( x�Cy�Cz ) R ( x�Cy�Cz )�@�ƂȂ鑽����R ( x�Cy�Cz )�����݂��邱�Ƃ������B |
[�l����]�@
�J���𗊂�ɒT�������Ȃ��B���܂肢�����Ƃ͂����܂���B
[��]�@
f (x�Cy�Cz)�{x��( y�{z )�~L
f (x�Cy�Cz)�{y��( z�{x )�~M
f (x�Cy�Cz)�{z��( x�{y )�~N �@ ( L�CM�CN �͑����� )
�Ƃ�����B���ӂ�
f (x�Cy�Cz)�ɂ��낦��ƁC�����̕ό`�͍��Z���x���ł��ȁB
f (x�Cy�Cz)�{( x�{y�{z )��( y�{z )�~( L�{1)
f (x�Cy�Cz)�{( x�{y�{z )��( z�{x )�~( M�{1)
f (x�Cy�Cz)�{( x�{y�{z )��( x�{y )�~( N�{1)�@
�ƕ\����B
������ f (x�Cy�Cz)�{( x�{y�{z ) ��y�{z�Cz�{x�Cx�{y �������ɂ��R�����Ȃ̂ŁC���̂悤�Ȃ��̂�
�P���߂�ƁC
�@�@�@f (x�Cy�Cz)�{( x�{y�{z )��(x�{y) (y�{z) (z�{x)�@ ������ł悢�̂ł��傤���H�ςȖ��B
�@�@�@f (x�Cy�Cz)��(x�{y) (y�{z) (z�{x)�|( x�{y�{z )
�i���j�@(x�{y) (y�{z) (z�{x)�|(x�{y�{z)
�@�@�@
|
�@�T�D�@�@�T�~�T�̃}�X�ڂ�����C���̂�������̂S�~�S�̃}�X�ڂ̊e�}�X�ɂP�C�Q�C�E�E�E�C�P�U�̐��� �@�@�@�̂����ꂩ���C�ǂ̂Q�}�X�ɏ����ꂽ�������قȂ�悤�ɏ������ށi���j�B��P�s�����S�s�� �@�@�@�e�s�ɂ��āC���̍s�ɏ����ꂽ�S�̐��̍��v�����̍s�̉E�[�̉���������Ă��Ȃ��}�X �@�@�@�ɏ������ށB�����悤�ɁC��P���S��̊e��ɂ��Ă��C���̗�ɏ����ꂽ�S�̐��� �@�@�@���v�����̗�̉��[�̉���������Ă��Ȃ��}�X�ɏ������ށB�E�����̃}�X�ɂ͉��������� �@�@�@�܂Ȃ��B �@�@�@�ȉ��̏��������ő�̐���m�����߂�B �@�@�@�@�@�����F�i���j�̒i�K�ł��܂������������ނƁC��T��ɁC�������܂ꂽ���̍���m�ȏ�� �@�@�@�@�@�@�@�@�Q�}�X�����݂��C��T�s�ɁC�������܂ꂽ���̍���m�ȏ�̂Q�}�X�����݂���B |
[�l����]�@
�Ⴆ�C���̂悤�ɂȂ�܂��B
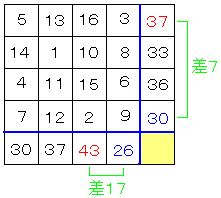
���̏ꍇ��m��7�ƂȂ�܂��B����m���Ȃ�ׂ��傫���������̂ŁC�ő�̗�ɂ͑傫�Ȑ����C
�ŏ��̗�ɂ͏����Ȑ������C���̒l���ύt����悤�ɂ��܂��B
[��]�@
|
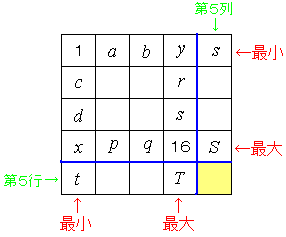
��T��ɏ����ꂽ�S���̂����C �@�ő吔��S�C�ŏ�����s�C ��T�s�ɏ����ꂽ�S���̂����C �@�ő吔��T�C�ŏ�����t �Ƃ��C�E�}�̂悤�Ɋe�}�X�̐����ł����B m���ő�ƂȂ�ꍇ�C�a���ŏ��̍s�C��̌�_�ɂ͂P���C�a���ő�̍s�C��̌�_�ɂ͂P�U������B �Ȃ��Ȃ�C������_�ɕʂ̐����������ꍇ�C���̐����P�C�P�U�ɂ��ꂼ�����ւ���C S�|s�܂���T�|t������ɑ傫���ł��邩��ł���B �����ŁC�@ |
|
�@�@�@�@�@ S�|s �� (p�{q)�|(a�{b)�{(x�|y)�{15
�@�@�@�@�@�@�@T�|t �� (r�{s)�|(c�{d)�|(x�|y)�{15
�ӁX�𑫂��ƁC
�@�@�@�@( S�|s )�{( T�|t )��(p�{q�{r�{s)�|(a�{b�{c�{d)�{30�@�����ꂪ�C�Â��ɂ������B
p�{q�{r�{s���ő�ƂȂ�̂́C12�{13�{14�{15��54�@��16�͂��łɎg���Ă���̂ŁB
a�{b�{c�{d���ŏ��ƂȂ�̂́C2�{3�{4�{5��14�@�@��1�͂��łɎg���Ă���̂ŁB
������C( S�|s )�{( T�|t ) ���ő�ƂȂ�l�́C54�|14�{30��70
S�|s�@�C T�|t �̂����̏��������i�傫���Ȃ����j��m�ƂȂ�̂ŁCm���ő�ɂȂ�̂́C
�@S�|s��35�C T�|t��35
�̂Ƃ��ł���B���̂悤�ɂȂ��́C���̏ꍇ������B
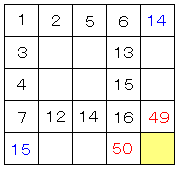
�i���j�@�R�T
|
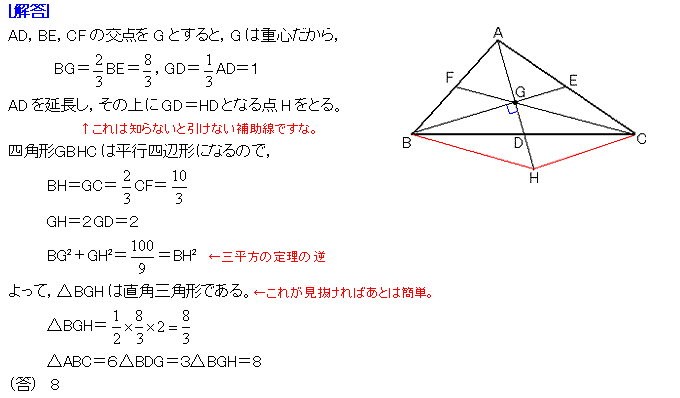
�@�U�D�@�@�O�p�`ABC�ɂ����āCBC�CCA�CAB�̒��_�����ꂼ��D�CE�CF�Ƃ���ƁCAD���R�CBE���S�C �@�@�@CF���T�ł���BABC�̖ʐς����߂�B |
[�l����]�@
AD���������āC���s�l�ӌ`�����܂��B
�@
|
�@�V�D�@�@�l�p�`ABCD�̑Ίp��AC�CBD�͎l�p�`�̓����̓_P�Ō�����Ă���B AC���Q�CBD���R�C��APB���U�O���ł���Ƃ��CAB�{BC�{CD�{DA�̂Ƃ肤��ŏ��l�����߂�B |
[�l����]�@
������⏕���������܂��B�Q�_�������̒������ŏ��ƂȂ�̂͐����̂Ƃ��ŁC����܂���
�S�ӂ̒����̘a���C���܂��u����������悤�ɂ��܂��B
[��]�@
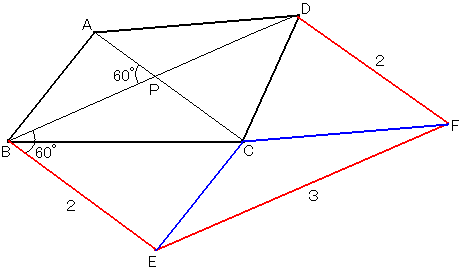
AC�ɕ��s�Œ�����AC�ɓ���������BE�CDF��}�̂悤�Ɉ����ƁC���Ȃ��Ȃ������ł��܂���ˁB
�l�p�`ABEC�CACFD�CBEFD�͕��s�l�ӌ`�ƂȂ�B
�����ŁCAB��CE�CAD��CF������C
AB�{BC�{CD�{DA��CE�{BC�{CD�{CF
�@�@�@�@�@�@�@�@�@�@�@�@���iBC�{CF�j�{�iDC�{CE�j�@�����܂����������B
���̘a���ŏ��ƂȂ�̂́C�l�ӌ`BEFD�̑Ίp���̌�_��C�ɂȂ�Ƃ��ł���B
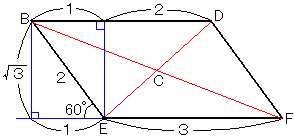
�}����C�ŏ��l�́C
![]()
�@�W�D�@�@n�͏\�̈ʂ��O�łȂ��S���̐��̐����ł���Cn�̏�Q���Ɖ��Q�������ꂼ��Q���̐����� �l�����Ƃ��C���̂Q���̐ς�n�̖ƂȂ�B���̂悤��n�����ׂċ��߂�B |
[�l����]�@
��Q����A�C���Q����B�Ƃ��āC�܂�A��B�̏��������܂��B
[��]�@
n�̏�Q����A�C���Q����B�Ƃ���ƁCn���P�O�OA�{B
���ꂪAB�̔{���ƂȂ邩��C�P�O�OA�{B��A�̔{���ł���B
����āCB��A�̔{��������CB��t A�@�it���P�C�Q�C�E�E�E�C�X�j�@���܂���A��B�̊W��z���B
�ƕ\����B
�܂��C�P�O�OA�{B��B�i��t A�j�̔{���ł����邩��C�P�O�OA��t A�̔{���C�܂�t�͂P�O�O�̖ł���B
����āCt���P�C�Q�C�S�C�T�@������ɏ��������ڂꂽ�B
���̂Ƃ��Cn���P�O�OA�{t A��A�i�P�O�O�{t�j������C���ꂪAB�̔{���ɂȂ�ɂ́C
B���P�O�O�{t�̖ɂȂ�ꍇ�����߂�悢�B
�i�A�j t���P�̂Ƃ��@�����ɒ��ׂĂ����B
�@�@�P�O�P�̂Q���̖͂Ȃ��B
�i�C�j t���Q�̂Ƃ�
�@�@�@B���QA�@������CB�͋����B��������o���Ă����ƒT���₷���B
�@�@�P�O�Q�̂Q���̖̂����C�����́C�R�S
�@�@�@�@�@B���R�S�CA���P�V�Cn���P�V�R�S
�i�E�j t���S�̂Ƃ�
�@�@�@B���SA�@������CB�͂S�̔{���B
�@�@�P�O�S�̂Q���̖̂����C�S�̔{���́C�T�Q
�@�@�@�@�@B���T�Q�CA���P�R�Cn���P�R�T�Q
�i�G�j t���T�̂Ƃ�
�@�@�@B���TA�@������CB�͂T�O�ȏ�̂T�̔{���ł��邪�C�P�O�S�̖ɂ���͂Ȃ��B
�i���j�P�R�T�Q�C�P�V�R�S
�@�X�D�@�@�P�X�~�P�X�̃}�X�ڂ�����B���ׂĂ̕ӂ��}�X�̋��E�ɉ����Ă��钷���`���u�ǂ������`�v �Ƃ������Ƃɂ���B���̏��������ŏ��̐���n�����߂�B �@�@�����F�ǂ̂悤�ɂX�̃}�X����菜���Ă��C�c��̕�����n�ȉ��̗ǂ������`�ɕ����ł���B |
[�l����]�@
��菜���}�X�����Ȃ����Ē��ׁC�K�����������܂��B
��菜���}�X���[�̗�ɂ���ꍇ�C��菜���}�X���[�̗�ɂȂ��ꍇ���������̐������Ȃ��B
�܂��C��菜���}�X��������ɂ���ꍇ�C��菜���}�X��������ɂȂ��ꍇ���������̐������Ȃ��B
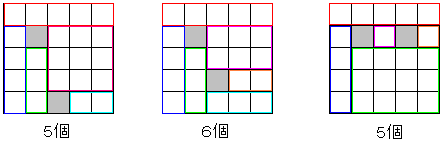
������C��菜���}�X�����ׂĒ[�ł͂Ȃ��C��������ɂȂ��ꍇ���l���܂��B
[��]�@
��菜���}�X�̐���m�Ƃ���B���̓�����m���X�̂Ƃ����l����悢�B
�܂��C��菜��m�̃}�X�����ׂĊ܂ށu�ǂ������`�v���l���C���̂����Ŗʐς��ŏ��̒����`��S�Ƃ���B
�����Ăr�̓�����ǂ������`�ŕ�������Ƃ��C�����ŏ��ƂȂ�悤�ɕ��������Ƃ��́C�����̌��̍�
��l��am�Ƃ���B
��������������ł��B�}�X�ڂ̎�菜�����̂��ׂĂ̏ꍇ�ׂ�Ƃ����O��ŁC�ǂ̏ꍇ���ǂ������`���ŏ��ɂȂ�悤�Ɉ͂ށB
���̂Ƃ��̊e�X�̗ǂ������`�̌��̂����̍ő�l��am�Ƃ���C�Ƃ������Ƃł��B
|
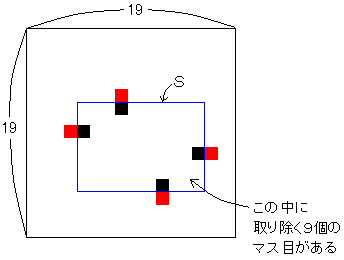
��菜���}�X�̂����C�r�̊e�ӂɐڂ�����̂����ꂼ�ꑶ�݂���B����Ƃr�̕ӂɂ��đΏ̂ȉE�}�̂悤�ȐԂ��}�X�����݂���ꍇ�C���̂ǂ̃}�X��S�̓����̗ǂ������`�Ɋ܂߂Ĉ͂ނ��Ƃ��ł��Ȃ��B ������C�S�̂�ǂ������`�ŕ�������ɂ� �iam�{�S�j�̒����`���K�v�ƂȂ�B ����ċ��߂�n�́C �@�@ n��a9�{�S �ƂȂ�B �����ŁCa9�����߂邽�߁Cam�����ɒ��ׂĂ����B |
|
�i�@�j�@m���R�̂Ƃ��@

�ǂ������`�̌����ŏ��ɂȂ�悤�Ɉ͂ނƂ��C���̐}�̏ꍇ�͂U�ł���B
�@����āC�@�@a3���U�@���ǂ̂悤�Ɉ͂�ł��ŏ��łU�ƂȂ������C�T�ł͈͂߂Ȃ����Ƃ������K�v������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���ꂪ�킩��Ȃ��E�E�B
�i�A�j�@m���S�̂Ƃ��@
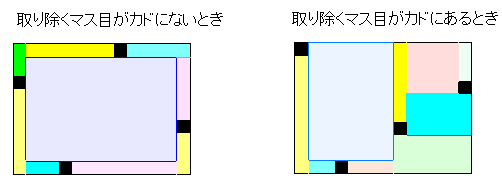
���̐}�̂悤�ɁCa4���X�ł���B���W�ł͈͂߂Ȃ����Ƃ������K�v������B������킩��Ȃ��B
���܁C��菜���}�X���P�lj������Ƃ��ɁC�������钷���`����������̂����l����B
�lj������}�X�ڂ��C�������Ă���ǂ������`�̂ǂ̕����ɂ���̂��Ŏ��̂R�ʂ�̏ꍇ������B
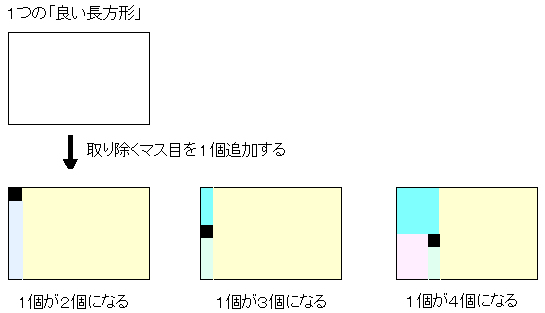
���̂悤�ɍő�łR������ꍇ�����肤��̂ŁC�ȉ�a5�Ca6�C�E�E�E�́C�R�������Ă����B
���������킩��Ȃ��B��ԉE�̏ꍇ�ł��C�S�̐V���������`�̂ǂꂩ������܂ł̒����`�Ɋ܂܂�Ă��܂�
���Ƃ�����C�u�R������v�Ƃ͌�����Ȃ��B����������K�v������̂ł����C���`�`��C����B
����āC�@�@a9��a4�{�R�~�i�X�|�S�j���Q�S
���߂�ŏ��̐���n�́C
�@�@�@�@�@�@�@n��a9�{�S���Q�S�{�S���Q�W
�i���j�@�Q�W