200�X�N�@���{�W���j�A���w�I�����s�b�N�\�I�@���Ɖ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@2009�N1��12���@��������3����
|
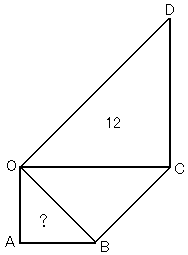
�@�P�D�@�@���}�ɂ����āC�O�p�`OAB�COBC�COCD�͂��ꂼ���OAB�C��OBC�C��OCD�p�Ƃ��� �@�@�@���p�ӎO�p�`�ł���B�O�p�`OCD�̖ʐς�12�̂Ƃ��C�O�p�`OAB�̖ʐς����߂�B �@�@�@�@�@ |
[�l����]�@
���p�ӎO�p�`���C�������܂��B
[��]�@
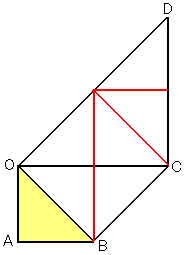
���̐}����C��OCD�́�OAB���S���ׂ����̂��Ƃ킩��B
��OAB��12��4��3
�i���j�@3
|
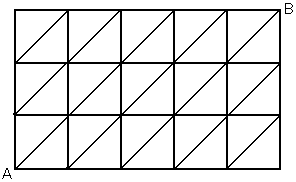
�@�Q�D�@�@���1�̐����`15����Ȃ�3�s5��̃}�X�ڂ�����B�ł������ɂ��钸�_��_A�C �@�@�@�ł��E��ɂ��钸�_��_B�Ƃ���B�܂��C�e�����`�ɂ͉��}�̂悤�ɍ����̒��_����E�� �@�@�@�̒��_�ւ̑Ίp����������Ă���B�����̑Ίp���Ɛ����`�̕ӂ�ʂ�A����B�ւ̍s�� �@�@�@���̂����C�������ŒZ�ł�����͉̂��ʂ肠�邩�B �@�@�@�@ �@�@�@ |
[�l����]�@
�܂��́C�ŒZ�����ƂȂ�����̎�ނ��l���܂��B�Ȃ�ׂ��Ίp���𑽂��ʂ��������������Z���Ȃ�̂ŁC
�Ίp��3�{�C���_2�{��ʂ�ꍇ���ŒZ�����ƂȂ�܂��B
[��]�@
�ŒZ�����ƂȂ�̂́C���}�̐Ԃ������̂�����5�{��ʂ�ꍇ�ł���B
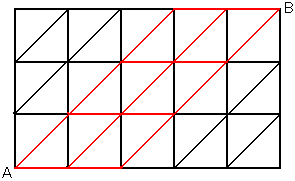
���_1�{�i�ނ��Ƃ��u���v�C�Ίp��1�{�i�ނ��Ƃ��u�^�v�Ƃ��Ă��̏������l����ƁC
�����^�^�^
���^���^�^
���^�^���^
���^�^�^��
�^�����^�^
�^���^���^
�^���^�^��
�^�^�����^
�^�^���^��
�^�^�^����
��10�ʂ�B��5�̂��̂���2������g�����Ɠ����ŁC5C2��10�ʂ�Ƃ��Ă��n�j�B
�i���j�@10�ʂ�
|
�@�R�D�@�@���̐��������ŕ\�����Ƃ��̐��������i�����_�ȉ���1�ʂ��̂Ă����j�����߂�B �@�@�@ |
[�l����]�@
�傴���ςɌ��ς���ƁC���ꁁ13,000,000��13�~106�C���q��109,000,000��109�~106�@���炢�ŁC
����������8�ɂȂ肻�����ƌ��������܂��B
[��]�@
���ꁁS�C���q��T �Ƃ���B
���q�̂��ꂼ��̐��ɂ��āC���̑傫���ׂ�ƁC
�@ �@�@ �@1�~8��9��1�~9�@�@�@�@�����q�̂P�̐��𗼃T�C�h�ł͂���
12�~8��98��12�~9
�@ �@123�~8��987��123�~9
1234�~8��9876��1234�~9
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@12345678�~8��98765432��12345678�~9
�����������āC
�@�@�@�@�@�@�@S�~8��T��S�~9
�e�ӂ�S�ł��ƁC
�@�@�@�@�@�@�@![]()
����āC����������8�ƂȂ�B
�i���j 8
|
�@�S�D�@�@3���̐��̐�����2����C�ǂ������̈ʂƏ\�̈ʂ��Ƃ���9�ł���B���̂悤��2�̐� �@�@�@�̐ς̐�̈ʂƂ��Ă��肤��l�����ׂċ��߂�B |
[�l����]�@
�S�̈ʂ̐����ł����āC���������ēW�J���܂��B
[��]�@
�S�̈ʂ̐���a�Cb�Ƃ���ƁC2���̐ς́C
(100 a�{99) (100 b�{99)��10000 ab�{9900 (a�{b)�{9801
��10000 ab�{10000(a�{b)�|100(a�{b) �{9801�@�@���ό`����
��100�o98�|(a�{b)�p�{1�{10000 ab�{10000(a�{b) �@���P�͖����ł���
��̈ʂɉe������̂͐Ԃ����������ł���C���߂���̂�98�|(a�{b) �̏\�̈ʂł���B
2��a�{b��18������C
�@�@�@�@80��98�|(a�{b)��96
98�|(a�{b)���\�̈ʂ�8��9�ł���B
�i���j�@8�C9
|
�@�T�D�@�@���ׂĂ̕ӂ̒�����1�̓ʌ܊p�`������C����2�{�̑Ίp���̂Ȃ��p��90���ł���B �@�@�@���̂悤�Ȍ܊p�`�̖ʐςƂ��Ă��肤��ő�̒l�����߂�B �@�@�@�������C���ׂĂ̓��p��180�������ł���܊p�`�̂��Ƃ�ʌ܊p�`�Ƃ����B �@�@�@ |
[�l����]�@
���ׂĂ̕ӂ�1��2�{�̑Ίp������������悤�Ȍ܊p�`�������Ă݂܂��B
[��]�@
���ׂĂ̕ӂ�1��2�{�̑Ίp������������悤�ȓʌ܊p�`�́C���̂悤�ɂȂ�B
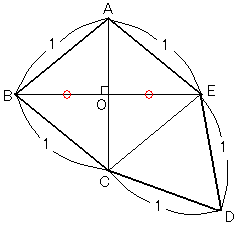
���̐}�ŁC
��ABO�߁�AEO�i���p�O�p�`�̎ΕӂƑ��̂P�ӂ��������j
������CBO��EO
����āC��BCO�߁�ECO�i�Q�ӂƂ��̊Ԃ̊p���������j
������CBC��EC��1�ƂȂ�C�l�p�`ABCE�͂Ђ��`�ł���B�����̂Ђ��`�̖ʐς��ő�ɂ�������B
�Ђ��`ABCE�̖ʐς́CBC�~�iA����BC�Ɉ����������̒���h�j�ł���C���ꂪ�ő�ɂȂ�̂�
h��1�̂Ƃ�������C�Ђ��`ABCE�̖ʐς̍ő�̒l�́C
�@�@1�~1��1 �������`�̂Ƃ��B���̂Ƃ��܊p�`ABCDE�͓ʌ܊p�`�ƂȂ�j
����C���O�p�`CDE�̖ʐς́C
�@�@![]()
����āC�܊p�`�̖ʐς̍ő�̒l�́C
�@�@�@![]()
![]()
|
�@�U�D�@14n�C16n�C18n�C20n�̐��̖̌������ׂē������Ȃ�悤�ȍŏ��̐��̐���n�� �@�@�@���߂�B |
[�l����]�@
�̌��̋��ߕ��ɂ́C���̌���������܂��B�i���Z���x���j
2a�~3 b�~5c�̖̌��́C(a�{1) (b�{1)
(c�{1)
�w�����P���������|�����킹�����̂��̌��ƂȂ�܂��B
[��]�@
14n��2�~7�~n
16n��24�~n
18n��2�~32�~n
20n��22�~5�~n
�����ŁCn��2a�~3
b�~5c�~7
d�Ƃ����B���ŏ��̐��̐��������߂�̂ŁC����ȊO�̈����͖������Ăn�j�B
�@�@14n ��
2a+1�~3
b�~5c�~7d+1�@�@�c�c�@
16n �� 2a+4�~3
b �~5c�~7d�@�@�c�c�A
18n �� 2a+1�~3
b+2�~5c�~7d�@�c�c�B
20n �� 2a+2�~3
b �~5c+1�~7d�@�c�c�C
�@�ƇA�̖̌����������̂ŁC
�@�@�@(a�{2)
(d�{2)��(a�{5)
(d�{1) �@��3 b�~5c�����ʂȂ̂Ŗ����ł���
a��3 d�{1�@�c�c�i�A�j
�A�ƇB�̖̌����������̂ŁC
�@�@�@(a�{5)
(b�{1)��(a�{2)
(b�{3) �@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@3b��2
a�{1
�@�@�@�@�@�@�@�@�@�@�@��2(3 d�{1)�{1�@���i�A�j����
b��2 d�{1
�c�c�i�C�j
�A�ƇC�̖̌����������̂ŁC
�@�@�@(a�{5)
(c�{1)��(a�{3)
( c�{2)
2c��a�{1
2c��3
d�{2 �c�c�i�E�j�@���i�A�j����
�i�A�j�`�i�E�j�����ŏ���n�́Cd��0�̂Ƃ��ŁC
�@�@�@�@a��1�Cb��1�Cc��1�@�@���̂Ƃ��Cn��2�~3�~5��30
�i���j�@30
|
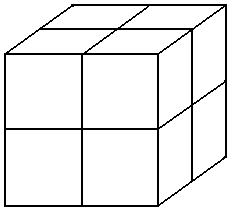
�@�V�D�@��ӂ̒�����1�̏������̂�8����B�������d�˂āC���}�̂悤�Ɉ�ӂ̒�����2�� �@�@�@�����̂�������B���̂Ƃ��C���Ƃ̏������̂̒��_�ƈ�v����_��2�_�ȏ�ʂ�悤�Ȓ��� �@�@�@�͋�ԓ��ɉ��{���邩�B �@�@�@�@�@ |
[�l����]�@
�S����27�̒��_������C���̒���2�_��ʂ钼�������{����̂������߂�����̂ł����C2�_
�łȂ�3�_�ʂ钼��������܂��B�d�����钼�������Ƃň����C�Ƃ������@�ŋ��߂܂��B
[��]�@H22 1.12�����B���w�E���肪�Ƃ��������܂��B
27�̒��_�̂�����2�_��ʂ钼���̖{���́C�d�����ӂ��߂āC
�@�@�@27�~26��2��351�i�{�j
���̒��ɂ́C2�_������ʂ钼����3�_��ʂ钼��������C3�_��ʂ钼����3��d�����Đ�������
����B���`�C�a�C�b���꒼����ɂ���ꍇ�C�����`�a�C�����a�b�C�����`�b�̂R���J�E���g����Ă���B
���ɁC3�_��ʂ钼���̖{�������߂�B
�����̂�1�̖ʏ�ɂ���3�_��ʂ钼���̖{���́C
�@�@�@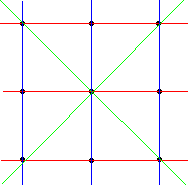
������C���v8�{�B
�����̂�6�̖ʂ̂����݂��ɐ�����3�̖ʂ��A�C�C�C�E�Ƃ��C���̂��ꂼ��ɕ��s�Ȓ����̖{��
�i�ʏ�̒������܂ށj�𐔂���B
�A�ɕ��s��3�_��ʂ钼���́C8�~3��24�i�{�j
�A�ɕ��s�łȂ��C�ɕ��s��3�_��ʂ钼���́C5�~3��15�i�{�j�@�����24�{�Ő��������̂͂̂����B
�A�ɂ��C�ɂ����s�łȂ��E�ɕ��s��3�_��ʂ钼���́C2�~3��6�i�{�j�@�����24�{�C15�{�Ő��������̂͂̂����B
����āC�����̍��v�́C24�{15�{6��45�i�{�j
��ӂ�2�̗����̂̑Ίp��4�{���C3�_��ʂ钼��������C������ӂ��߂āC���v49�{�B
����āC���߂钼���̖{���́C
�@�@351�|49�~2��351�|98��253�i�{�j�@���S�̂���C�d������3�̂�����2���������B
�i���j�@253�{
|
�@�W�D�@1�ȏ�100�ȉ��̊�����ׂĊ|�����킹�����̉�3�������߂�B |
[�l����]�@
1����99�܂ł̊��50����܂��B�����S���|���Čv�Z����킯�ɂ͂����܂���B
��3���Ƃ́C�|�����킹���ς�1000�ł�����Ƃ��̗]��Ȃ̂ŁC1000��8�~125�ƍl����8�ł�����]��
�ׂ܂��B
[��]�@
1�ȏ�100�ȉ��̊50�̐ς�T�Ƃ���B
T�̉�3���̐��́CT��1000�ł�����Ƃ��̗]��ł���B
�����ŁC1000��8�~125�ł���CT��125�ł����B
�@�@T���i5��25�������P����99�܂ł̊�̐��j�~5�~25
�ƍl���C�i�@�j���̒l��8�ł�����]����l����B
���܁C
1�~3�~7��21��8�ł�����]�聁5
�܂��C
9�~11�~13�~15���i8�{1�j�i8�{3�j�i8�{5�j�i8�{7�j��8�~�i�����j�{1�~3�~5�~7
�ƕ\�����̂ŁC
9�~11�~13�~15��8�ł�����]�聁1�~3�~5�~7��8�ł�����]�聁1�@��4���Z�b�g�ɂ���̂��|�C���g�ł��B
���l�ɁC
17�~19�~21�~23��8�ł�����]�聁1�~3�~5�~7��8�ł�����]�聁1
27�~29�~31��8�ł�����]�聁3�~5�~7��8�ł�����]�聁1�@�@��25�͏������C�����]��ɂȂ�B
33�~35�~37�~39��8�ł�����]�聁1�~3�~5�~7��8�ł�����]�聁1
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E ���ȉ������B
89�~91�~93�~95��8�ł�����]�聁1�~3�~5�~7��8�ł�����]�聁1�@�������܂ŁC�S��1�ɂȂ�B
97�~99��8�ł�����]�聁1�~3��8�ł�����]�聁3
�ȏ���C�i5��25�������P����99�܂ł̊�̐ρj��8�ł�����]��́C��L�̗]������ׂĂ���
���킹�āC�@�@5�~1�~1�~�E�E�E�~1�~3��15
�����8�ł�����]��ɓ������̂ŁC7�ƂȂ�B
����āC
�@�@�@�i5��25�������P����99�܂ł̊�̐ρj��8 M�{7
�Ə����āC
�@�@�@T���i8 M�{7�j�~5�~25��1000 M�{875
T��1000�ł�����Ƃ��̗]���875������CT�̉�3���̐��́C875
�i���j�@875
|
�@�X�D�@�O�p��O-ABC�ƒ��ABC��̓_X�́COA��2�COB��3�COC��4�C��AOB����BOC�� �@�@�@��COA�C��AOX����BOX����COX��30�����݂����Ă���B���̂Ƃ��O�p��O-ABC�̑̐ς� �@�@�@���߂�B�������CPQ�Ő���PQ�̒�����\�����̂Ƃ���B |
[�l����]�@
ABC���ʂƂ��ė��̂������̂͂킩��ɂ����BOX�ƁCOA�COB�COC�̂Ȃ��p��30���Ȃ̂ŁC�܂���
OA�COB���̂��Đ��O�p��������܂��B
[��]�@
OA�COB����������OA1��OB1��4�ƂȂ�_A1�CB1���Ƃ�B
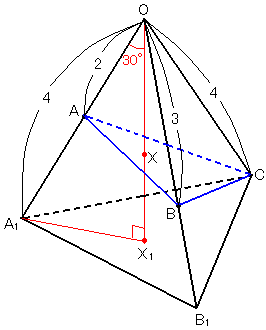
��OA1B1�߁�OB1C�߁�OCA1�@���Q�ӂƂ��̊Ԃ̊p���������B
������CA1B1��B1C��CA1
����āC��A1B1C�͐��O�p�`�ł���C�O�p��OA1B1
C�͐��O�p���ł���B
OX�Ɓ�A1B1C�̌�_��X1�Ƃ���ƁC��A1O X1����B1O X1����CO X1��30��������C
��OA1X1�߁�OB1
X1�߁�OC X1�@���Q�ӂƂ��̊Ԃ̊p���������B
����āC A1X1��B1X1��CX1
X1�́�A1B1C�̏d�S�ƂȂ�̂ŁCOX1�ہ�A1B1C
��OA1X1�ŁC�@A1X1��2
![]()
��A1B1C�͐}�̂悤�ɂȂ�B
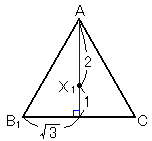
���O�p��OA1B1 C�̑̐ς́C
�@�@�@![]()
���ɁC�O�p��OABC���O�p��OA1B1
C�̑̐ς̔���l����B
�܂��C��OAB�F��OA1B1���i2�~3�j�F�i4�~4�j��3�F8
���͂��ފp�������Ȃ̂ŁC�Q�ӂ̐ς��ʐς̔�ƂȂ�B
�������ʂƌ���ƁC�������������̂ŁC�̐ς̔���R�F�W�ƂȂ�B
����āC�O�p��O-ABC�̑̐ς́C
�@�@�@![]()
![]()
|
�@�P�O�D�@���� a�C b�C c�C
d�C
e�C
f �� �@�@�@�@�i
a�{1999 �j�i b�|1999 �j�i c�{1999 �j�{�i d�|1999 �j�i e�{1999 �j�i�@f �|1999 �j��1 �i a�{2000 �j�i b�|2000 �j�i
c�{2000 �j�{�i d�|2000 �j�i e�{2000 �j�i�@f �|2000 �j��10 �i a�{2001 �j�i b�|2001 �j�i
c�{2001 �j�{�i d�|2001 �j�i e�{2001 �j�i�@f �|2001 �j��100 �@�@�@���݂����Ƃ��C �i a�{2009 �j�i b�|2009 �j�i
c�{2009 �j�{�i d�|2009 �j�i e�{2009 �j�i�@f �|2009 �j �@�@�@�����߂�B |
[�l����]�@
�������G�łS���̐�������̂ŁC�u�����������Ă��������V���v���ɂ��܂��B
[��]�@
a�{2000��A�Cb�|2000��B�Cc�{2000��C�Cd�|2000��D�Ce�{2000��E�Cf �|2000��F �Ƃ����ƁC
�R�̏����̎��́C
�@�@�@�@�i A�|1 �j�i�@B�{1 �j�i C�|1�@�j�{�i D �{1 �j�i E�|1 �j�i�@F�{1 �j��1�@�c�c�@
A B C�{D E F ��10�@�c�c�A
�@�i A�{1 �j�i�@B�|1 �j�i C�{1�@�j�{�i D�|1 �j�i E�{1 �j�i�@F�|1 �j��100�@�c�c�B
���߂鎮�́C
�@�@�@T ���i A�{9 �j�i�@B�|9 �j�i C�{9�@�j�{�i D�|9 �j�i E�{9 �j�i�@F�|9 �j
�ƂȂ�B
�@���C
�@A B C�{�i�|A B�|B C�{C A �j�{�i�|A�{B�|C �j�{D E F�{�i
D E�{E F�|F D �j�{�i�|D�{E�|F �j��1
��������ƁC
�@�i A B C�{D E F�j�|�iA B�{B C�|C A�|D E�|E F�{F D�@�j�|�iA�|B�{C�{D�|E�{F �j��1
�@�@�iA B�{B C�|C A�|D E�|E F�{F D�@�j�{�iA�|B�{C�{D�|E�{F �j��9�@�c�c�C�@���A����
�B���C
�@A B C�{�iA B�{B C�|C A �j�{�i�|A�{B�|C �j�{D E F�{�i�|D E�|E F�{F D �j�{�i�|D�{E�|F �j��100
��������ƁC
�@�i A B C�{D E F�j�{�iA B�{B C�|C A�|D E�|E F�{F D�j�|�iA�|B�{C�{D�|E�{F �j��100
�@�@�iA B�{B C�|C A�|D E�|E F�{F D�j�|�iA�|B�{C�{D�|E�{F �j��90�@�c�c�D�@���A����
�C�C�D�������āC
�@�@A B�{B C�|C A�|D E�|E F�{F D��99��2��49.5
A�|B�{C�{D�|E�{F���|81��2���|40.5
����āC
�@�@T ��A B C�{9�iA B�{B C�|C A �j�{81�i�|A�{B�|C �j�{D E F�{9�i�|D E�|E F�{F D �j�{81�i�|D�{E�|F �j
���i A B C�{D E F �j�{9�iA B�{B C�|C A�|D E�|E F�{F D�j�|81�iA�|B�{C�{D�|E�{F �j
��10�{9�~49.5�|81�~�i�|40.5�j
�����߂��l������ł���
�@�@�@ ��3736
�i���j 3736
�c��͂f�v�����ɂt�o���܂��E�E�B