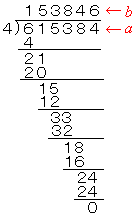2008年 日本数学オリンピック予選 問題と解答
2008年1月14日 試験時間3時間
|
1. 4つの相異なる1桁の正の整数がある。これらの最小公倍数として考えられる最大の値を 求めよ。 |
[考え方]
互いに素となる数を選んだ方が,公倍数は大きくなります。
[解答]
1~9までの9個の整数の最小公倍数は,23×32×5×7=2520
4つの相異なる1桁の正の整数について,その最小公倍数はこれ以下である。
ここで5,7,8,9を選ぶと,この4数の最小公倍数は, 5×7×8×9=2520
(答) 2520
|
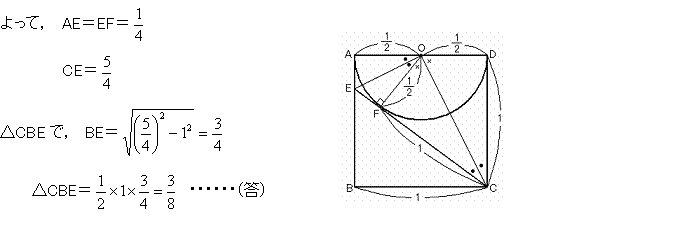
2. 一辺1の正方形ABCDがある。ADを直径とする円をOとし,辺AB上の点Eを,直線CE がOの接線となるようにとる。このとき,三角形CBEの面積を求めよ。 |
[考え方]
BEがわかれば面積もわかります。
[解答]
右図で,AE=EF,CD=CF=1
∠COE=90°だから,△OEF∽△COF
|
3. 太郎君は,1000円札と100円玉と10円玉と1円玉を1枚ずつ持って買い物に行き,ある 品物を買って,4枚すべてを支払いに用いた。品物の価格として考えられる値は何通りあるか。 ただし,太郎君は,自分の支払うお金と釣り銭とに共通のものがないような支払い方のうち, 釣り銭を渡された後の手持ちのお金の枚数が最小になるようなやり方を選ぶものとする。 なお,釣り銭は枚数が最小になるように渡されるものとする。また,お釣りが0円であることも ある。 |
[考え方]
題意が読み取りにくい。ようするに残った小銭を少なくしたいということです。例えば,品物の価格が,
・600円の場合, 1000+100+10+1=1111円を支払って,お釣りが511円だから,500円玉,10円
玉,1円玉が1枚ずつ戻る。これは「自分の支払うお金と釣り銭とに共通のものがない」という支払い
方になっていないので,適さない。
・606円の場合, 1000+100+10+1=1111円を支払って,お釣りが505円だから,500円玉,5円玉
が1枚ずつ戻る。←釣り銭は枚数が最小になるように渡されるので,この場合100円玉や1円玉では来ない。
「自分の支払うお金と釣り銭とに共通のものがない」という支払い方になっており,しかもこれは,他の
どの支払い方よりも後の手持ちの枚数が少ない。ので適する。
↑手持ちの枚数は3枚。1000円札1枚や1001円で支払うと,これよりも手持ちが多くなってしまう,ということ。
[解答]
支払うお金と釣り銭とに共通のものが存在しないから,釣り銭は100円玉,10円玉,1円玉では返って
こない。よって釣り銭がある場合,これらが5枚集まって500円玉,50円玉,5円玉のどれかとなる。
ただし,それぞれが2枚以上になると,1000円札または100円玉または10円玉が含まれてしまう。
よって,釣り銭としてあり得るのは,500円玉,50円玉,5円玉が高々1枚含まれる場合で,
0円 5円 50円 55円 500円 505円 550円 555円
である。
(答) 8通り
|
4. 正の整数であって,その正の約数のうち4で割った余りが2でないようなものの総和が 1000であるものをすべて求めよ。 |
[考え方]
4で割った余りが2であるものとは,2×(奇数)の形の数です。これを全体の和から除きます。
例えば72の場合,72=23×32だから,約数の総和は,
(1+2+22+23)×(1+3+32)=15×13=195
となり,このうち4で割った余りが2となるものを除くと,約数の総和は,
(1+2+22+23)×(1+3+32)-2×(1+3+32)=(1+22+23)×(1+3+32)=13×13=169
となります。
この値が1000となるように,数を定めるわけです。
[解答]
正の整数Nを素因数分解して,N=2a 3b 5c 7d ・・・ となったとする。(a,b,c,・・・は負でない整数)
正の約数のうち4で割った余りが2でないものの総和は,
(1+22+23+・・・+2a )×(1+3+32+・・・+3b )×(1+5+52+・・・+5c )×・・・
これが1000となるようにa,b,c,・・・を定める。
そこで( )内の和が1000の約数4,5,8,10,20,25,40,50,100,125,200,250,500,1000となる
場合を調べていくと,次の黄色の数があてはまる。
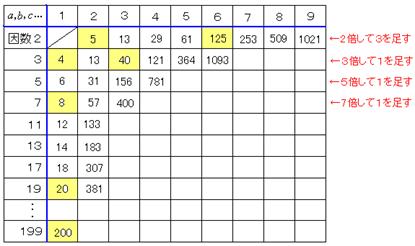
1000=4×250=5×200=8×125=20×50だから,当てはまる場合は,
5×200=(1+22)×(1+199)
8×125=(1+7)×(1+22+23+・・・+26)
のみ。
この整数は, 22×199=796, 7×26=448
(答) 448,796
|
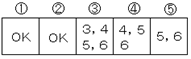
5. 2,3,4,5,6の数が書かれたカードが1枚ずつ,合計5枚ある。これらのカードを無作為 に横一列に並べたとき,どのi =1,2,3,4,5に対しても左からi番目のカードに書かれた 数がi以上となる確率を求めよ。 |
[考え方]
並べる数を左から考えていくと場合分けが必要になる。ので,並べる数を右から考えていく。
[解答]
|
右端には,5か6 右から2番目には,4か5か6 右から3番目には,3か4か5か6 が入ればよい。 この確率は, |
|
![]()
|
6. 正の整数nの十進法表記をn(10)で表す。相異なる正の整数a,b,cは次の条件をすべて 満たす。 ・ c(10)はa(10)から6を1つ取り除いたものと一致する。 ・ c(10)はb(10)から6を1つ取り除いたものと一致する。 ・ aとbの桁数は等しく,aはbの倍数である。 cとしてありうる最小のものを求めよ。 |
[考え方]
例えば,a,b,cの関係はa=612345,b=123645,c=12345のようになっており,このうち,aが
bの倍数になるものを求めればよいことになります。いろいろと数を書いて調べると,aの先頭は6となる
ことが予想できるので,あとは実際に割り算をしてしらみつぶしに調べます。これがどうも一番早い感じ。
[解答]
aはbの倍数で異なる数なので,a≧2bである。よって,(aの最高位の数)≧(bの最高位の数)×2となる
ので,aとbの最高位の数は異なり,aの最高位の数は取り除かれるべき数6だと決まる。
これにより,bの最高位の数は,1,2,3のいずれかで,aがbの何倍になるかを考えれば,次の場合に
絞られる。
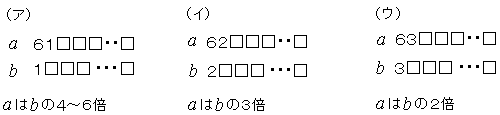
|
それぞれの場合のaを,倍数で実際に割り算する。 例えば(ア)でa=4bのとき,aを4で割り,商に立つ数を 順にaの次の位に当てはめていくと,右のようになる。 このとき, a=615384 b=153846 c=15384 となり,条件を満たす。 |
|
*bの高い方の位から順に数字が決まり,この数字がaの位に落ちるので,計算の途中で任意に「6」を入れることはできない。
なので,この方法で割り切れ,かつbの位のどこかに「6」があるものが,条件を満たすことになる。
上記以外の場合は,(ア)で2通り,(イ),(ウ)でそれぞれ1通りの計4通りあるが,同様にそれぞれ調べると,
いずれも満たすcが存在しない。
(答) 15384
|
7. 6桁の平方数の上3桁として考えられるものは全部でいくつあるか。 |
[考え方]
連続する平方数について,上3桁が同じになるか異なるかを調べると,
4002=160000,4012=160801のように同じ場合もあれば,
5002=250000,5012=251001のように異なる場合もあります。この違いをまず調べます。
[解答]
Nを自然数とし,平方数をN 2とすると,100000≦N 2<1000000
よって, 317≦N≦999
ここで,連続する平方数の差を調べると,(N+1)2-N 2=2N+1だから,
(ⅰ) 317≦N≦499のとき,(N+1)2-N 2<1000
(ⅱ) 500≦N≦999のとき,(N+1)2-N 2>1000
となる。
(ⅰ)のとき,平方数の上3桁の最小値は100,最大値は249であり,この間の値のすべてを取りうる。
なぜなら,N 2と(N+1)2で上3桁が2以上異なるとすれば,(N+1)2-N 2≧2000-999=1001
となり,条件に反するから。 ↑下4桁の差の最小値
よって,平方数の上3桁として考えられるものは,249-100+1=150(個)
(ⅱ)のとき,平方数の上3桁は,どれも異なる。
なぜなら,N 2と(N+1)2で上3桁が等しいとすれば,(N+1)2-N 2≦999-0=999となり,
条件に反するから。 ↑下4桁の差の最大値
よって,平方数の上3桁として考えられるものは,999-500+1=500(個)
(ⅰ)と(ⅱ)で上3桁の数字が一致するものはないので,加えて,650個。
(答) 650個
|
8. 8枚の硬貨がすべて表を向いて横一列に並んでいる。次の条件を満たす表向きの硬貨を 無作為に1枚選んで裏返す。 条件:その硬貨より右に裏向きの硬貨が1枚もない,もしくは,その硬貨より左に裏向きの 硬貨が1枚もない。 条件を満たす表向きの硬貨がなくなるまでこの操作を続けたとき,裏向きになっている硬貨 の枚数の期待値を求めよ。 |
[考え方]
裏向きになっている硬貨がk枚となる確率をそれぞれ求め,期待値の公式に当てはめればよいのです
が,この確率を求めるのがかなり難しい。なのでこれ以外の方法を考えることになります。
「裏向きになっている硬貨の枚数の期待値」とは,「それぞれの硬貨が裏向きになる期待値」をすべて
加えたものになります。なので1枚ずつに着目し,その硬貨が裏向きになる確率を求めます。
[解答]
この試行を次のように考える。←確率を求めやすいように,試行を変える。
8枚の硬貨を左から順に1,2,3,・・・,8と番号をつけ,この番号の順列をつくる。
その順列の順番に硬貨を裏返していく。途中,裏返せない硬貨があればそのままにする。
例えば,順列が「31684257」なら,
○○●○○○○○⇒●○●○○○○○⇒●○●○○●○○⇒●○●○○●○●
となり,裏向きになっている硬貨の枚数は4である。
このような試行を行ったとき,裏向きになった硬貨の枚数の期待値を求めればよい。
1~8の番号の順列を無作為につくったとき,番号kの硬貨が裏向きになる確率をak とする。
ak を求めるため,次の事象を設定する。
A : 番号kの硬貨の右にあるどの硬貨よりも,番号kの硬貨が先に裏向きになる。
B : 番号kの硬貨の左にあるどの硬貨よりも,番号kの硬貨が先に裏向きになる。
事象Aは,1~8の順列をつくったとき,番号kが番号k+1~8より前に並ぶ確率である。

|
9. 2008個の実数x1,x2,・・・,x2008 があり,|x1|=999であって,2以上2008以下の整数 nに対し,| xn |=| xn-1+1 | が成り立っている。このとき,x1+x2+・・・+x2008としてありうる 最小の値を求めよ。
|
[考え方]
絶対値の等式は2乗するとその記号をなくせます。また,階差の形の式を1~nまで足せば,途中の項が
消える。このことに着目して,和を,閉じた式で表すことを考えます。
[解答]
S=x1+x2+・・・+x2008とする。
| xn |=| xn-1+1 | ・・・・・・(ア)
この両辺を2乗すると,xn 2=xn-12+2 xn-1+1
xn 2-xn-12=2 xn-1+1 ←左辺が階差の形にする。
便宜上,x2009も(ア)で定義しておく。上の等式のnに2~2009までを代入し,
x2 2-x12=2 x1+1
x3 2-x22=2 x2+1
x4 2-x32=2 x3+1
・・・・・・・・
x2009 2-x20082=2 x2008+1
辺々を加えると,
x2009 2-x12=2 S+2008
x2009 2-9992=2 S+2008
2S=x2009 2-1000009 ・・・・・・(イ) ←x2009が最小になる場合を考えればよい。
ここでx1は奇数で,(ア)よりxnとxn-1の偶奇は異なるので,x2009は奇数である。だから,(イ)でSが最小
になるのは |x2009 |=1のときで,このとき,S=-500004となる。
|x2009 |=1,すなわちx2008 =0となる場合があるかどうかを調べると,←もしこういう場合がなかったら,困るな。
x1=-999としてxn =xn-1+1を使うと,x1000=0となるので,ここからxn =-(xn-1+1)とxn =xn-1+1を
交互に使えば,x1001=-1,x1002=0,x1003=-1,x1004=0,・・・となり,偶数番が0となる数列が作れる。
すなわちx2008 =0となる場合がある。←あってよかったです。
(答) -500004
|
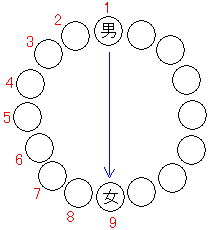
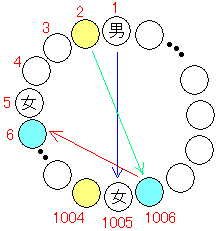
10. 2008人の男子と2008人の女子が集まってプレゼント交換をする。男子は花束を,女子 はチョコレートをプレゼントとして用意し,円形に並べられた椅子に全員が内側を向いて座る。 このとき,「持っているプレゼントを全員同時に右隣の人に渡す」という動作を何回か繰り返す と,男子全員がチョコレートを,女子全員が花束を持っている状態になった。男子が座っている 椅子の組合せとして考えられるものは何通りあるか。
|
[考え方]
「男子が座っている椅子の組合せ」というのが,紛らわしい表現です。椅子の組合せなので男子はいちいち
区別しなくていいと思うのですが,椅子を区別するのかしないのか?
(A) 4016個の椅子を区別する場合
これだと回転して同じ並びになる場合でも,異なるものと考えることができます。
(B) 4016個の椅子を区別しない場合
これだと回転して同じ並びになる場合は,同じものと考えることになります。
高校の教科書で円順列を扱う場合,暗黙の了解で(B)なのですが,(B)で解くには問題が難しすぎます。
どちらにしても,きちんとした数で答えることができず,累乗の和で表すしかないのが腑に落ちないところ。
[解答]
男子全員が花,女子全員がチョコレートを持っている状態を「原形」
男子全員がチョコレート,女子全員が花を持っている状態を「完成形」と呼ぶ。
n回の操作で完成形になったとする。
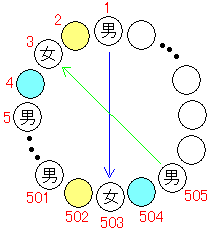
このとき,男子Aの花が女子aに渡り,女子aのチョコレートが男子Bに渡ったとすると,
2 n回の操作では,男子Aの花が男子Bに渡るので原形に戻り,3 n回の操作では再び完成形となる。
よって, n×(奇数)回で完成形になり,n×(偶数)回で原形に戻ることがわかる。
1周するのに4016回の操作を行うが,これで原形に戻るので,n×(偶数)=4016を満たす場合がある。
4016=24×251だから,nのとる値は,n=1,2,4,8,251,502,1004,2008
ここで,251=1×251,502=2×251,1004=4×251,2008=8×251だから,n=1,2,4,8でそれぞれ
完成形になった場合,これらの奇数倍(251倍)であるn=251,502,1004,2008でも,完成形となる。
よって,n=251,502,1004,2008のときの椅子の全組合せを求めればよい。
(A)のとき,←椅子に区別がつく場合。これだと易しい。
椅子に1~4016番までの番号をつける。各nについて,1~n番までの男女の椅子の組合せを決めれば,
残りの椅子には男子のn番先に女子が,女子のn番先に男子が来るようにすればよい。
だから,各nについての椅子の組合せの数は,2n通り。
よって,求める組合せの数は,
2251+2502+21004+22008通り
(答) 2251+2502+21004+22008通り
(B)のとき,←椅子に区別がつかない場合。これは難解。
各nについての椅子の組合せの数をanとする。まず,n=1,2,4,8のときを求める。
n=1のときは,男女交互に並ぶ場合しかないので,a1=1
n=2のときは,男男女女・・・と並ぶ場合しかないので,a2=1
n=4のときは,男男男男女女女女・・・と並ぶ場合と,男男女男女女男女と並ぶ場合があるので,a4=2
n=8のとき,
男女8人ずつ計16人で,男女が向かい合って座る場合が何通りあるかを求めればよい。
|
まず椅子に番号をつけ,1番に男子を置く。 2~8番までの男女の決め方は,27通り。←残りの椅子は確定する。 1つの並びに対して,これを左にmだけ回転させた場合に元の 並びと重なったとする。(1≦m<16) ←重複する場合を考える。 この回転を何回か繰り返せば1周し,元に戻るので,mは16の 約数である。ところがm=8では一致しないので,mは8の約数 ではない。よって,このようなmは存在しない。 これにより, 27通りの座り方に対して,回転させて重なる並びは ない。そこで図の番号をなくせば,円順列として生じる8通りの 並び(実際には同じ並び)が,27通りの中にカウントされている ことになる。よって,座り方の総数は, a8=27÷8=16 |
|
ふう。
n=251のとき
同様に,男女251人ずつ計502人で,男女が向かい合って座る場合が何通りあるかを求める。
まず,1番に男子を置く。2~251番までの男女の決め方は,2250通り。
1つの並びに対し,これを左にmだけ回転させた場合に元の並びと重なったとする。(1≦m<502)
このとき,mは502の約数であり,251(素数)の約数でないので,m=2
これは男女交互に並ぶ場合であるので,1通りしかない。
m=2のとき以外の場合は(2250-1)通りあるが,この中には,円順列として生じる251通りの並びが
重複してカウントされている。だから,重複しない並び方は,
(2250-1)÷251通り
よって,座り方の総数は,
a251=1+(2250-1)÷251 ←フェルマーの小定理から,2250≡1(mod251)。つまり2250-1は251の倍数。
n=502のとき
男女502人ずつ計1004人で,男女が向かい合って座る場合が何通りあるかを求める。
|
1番に男子を置く。2~502番までの男女の決め方は,2501通り。 前述と同様にmを求めると,mは1004の約数であり,502の約数でないので,m=4 番号Xに対し, X≡1(mod4)のとき,男 X≡503≡3(mod4)のとき,女 であり,X=2とX=504≡4は異性である。 よって,m=4のときの並び方は,2通りある。 ところが,これらはどちらも男男女女・・・という並びだから,実際に は1通りである。 m=4のとき以外の場合は(2501-2)通りあるが,この中に重複 してカウントされたものが502通りずつある。だから,重複しない 並び方は, (2501-2)÷502通り よって,座り方の総数は, a502=1+(2501-2)÷502=1+(2500-1)÷251 |
|
ふう・・。ツラい。
n=1004のとき
男女1004人ずつ計2008人で,男女が向かい合って座る場合が何通りあるかを求める。
|
1番に男子を置く。2~1004番までの男女の決め方は,21003通り。 同様にmを求めると,mは2008の約数であり,1004の約数でないので,m=8 番号Xに対し, X≡1(mod8)のとき,男 X≡1005≡5(mod8)のとき,女 であり,X=2とX=1006≡6は異性, X=3とX=1007≡7も異性 X=4とX=1008≡8も異性 である。 よって,m=8のときの並び方は,2番~4番を決める方法だけ あり, 23通り。 ところが,この並びは実際にはa4と同じだから,2通りである。 m=8のとき以外の場合は(21003-23)通りあるが,この中に重複 してカウントされたものが1004通りずつある。だから,重複しない 並び方は, (21003-23)÷1004通り よって,座り方の総数は, a1004=2+(21003-23)÷1004=2+(21001-2)÷251 |
|
ふう・・。やめたい。
n=2008のとき
男女2008人ずつ計4016人で,男女が向かい合って座る場合が何通りあるかを求める。
1番に男子を置く。2~2008番までの男女の決め方は,22007通り。
同様にmを求めると,mは4016の約数であり,2008の約数でないので,m=16
番号Xに対し, X≡1(mod16)のとき,男 X≡2009≡9(mod16)のとき,女
であり,異性となる組は,X=2,3,・・・,8に対し,順に,X=9,10,・・・,15である。
よって,m=16のときの並び方は,2番~8番を決める方法だけあり, 27通り。
ところが,この並びは実際にはa8と同じだから,16通りである。
同様に計算すると,座り方の総数は,
a2008=16+(22007-27)÷2008=16+(22004-16)÷251
やっとテンパった。
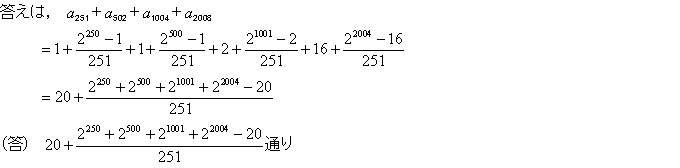
|
|
[考え方]
中点があるので,他の線分の中点も取って考えます。
[解答]
辺AB,ADの中点をそれぞれP,Qとする。

|
12. 正の整数の組( n,a1,a2,・・・,an )はa1+a2+・・・+an=2008を満たす。 Ak=a1a2・・・ak とするとき,A1+A2+・・・+An のとりうる最大の値を求めよ。 |
[考え方]
小さい数で調べてみると,和が8の場合,(a1,a2,・・・,an)が
(2,3,3)なら,2+6+18=26
(3,3,2)なら,3+9+18=30
なので,前に大きな数を持ってきた方が大きくなり,
(4,3,1)なら,4+12+12=28
(5,3)なら,5+15=20
(2,2,2,2)なら,2+4+8+16=30
なので,あまり大きな数を使わない方がよいようです。
[解答]
A1+A2+・・・+Ak=Tk とおき,組(a1,a2,・・・,an)に対するA1+A2+・・・+An=Tnの値を,それぞれの
名に応じて〔ア〕のように書く。
まず,次の2つの組を考える。
(ア) (a1,a2,・・・,ak,p,q,ak+3,・・・,an)
(イ) (a1,a2,・・・,ak,q,p,ak+3,・・・,an) ←2個だけが入れ替わった場合
それぞれのTn の値は,
〔ア〕=Tk +Ak・p+Ak・pq+Ak・pq ak+3+Ak・pq
ak+3 ak+4+・・・+An
〔イ〕=Tk +Ak・q+Ak・qp+Ak・qp
ak+3+Ak・qp ak+3 ak+4+・・・+An ←第k+1項だけが異なる
となるので,〔ア〕-〔イ〕=Ak・(p-q)。
よって,p>qならば〔ア〕>〔イ〕だから,値a1,a2,・・・,anでは,より大きな数を前に持ってきた方が,
和Tnは大きくなる。
次に, p+q=rとして,次の2つの組を考える。←2個と1個ではどちらが大きくなるかを調べる。
(ウ) (a1,a2,・・・,ak,p,q,ak+3,・・・,an)
(エ) (a1,a2,・・・,ak,r,ak+3,・・・,an)
このとき,
〔ウ〕=Tk +Ak・p+Ak・pq+A k・pq ak+3+Ak・pq ak+3ak+4+・・・+An
〔エ〕=Tk +Ak・r +Ak・r ak+3 +Ak・r ak+3ak+4 +・・・+An
だから,
〔ウ〕-〔エ〕=Ak・{
p+pq-r+(pq-r)(ak+3+ak+3ak+4+・・・+ak+3・・・an)}
=Ak・{
q(p-1)+(pq-r)(ak+3+ak+3ak+4+・・・+ak+3・・・an)}
ここで,pq-r=pq-(p+q)=(p-1)(q-1)-1だから,
p≧2,q≧2ならば,〔ウ〕>〔エ〕
よって,値a1,a2,・・・,anの中に4以上の数があれば,これを2以上の複数個の和に分けた方が,
和Tnは大きくなる。
以上のことから,Tnの最大値は,値a1,a2,・・・,anがすべて3以下の数で,これを大きい方から順に
並べたものである。この場合に限定して和Tnを考えていく。
次に,値a1,a2,・・・,anの中に2や1が何個含まれる場合が最大かを考える。
(オ) (a1,a2,・・・,ak,3,3,2,ak+4,・・・,an)
(カ) (a1,a2,・・・,ak,2,2,2,2,ak+4,・・・,an)
このとき,
〔オ〕=Tk +Ak・3+Ak・9+Ak・18+A k・18ak+4+A k・18ak+4ak+5+・・・+An
〔カ〕=Tk +Ak・2+Ak・4+Ak・8+Ak・16+A k・16ak+4+A k・16ak+4ak+5+・・・+An
だから,
〔オ〕-〔カ〕=2Ak・(ak+4+ak+4ak+5+・・・+ak+4・・・an)}>0
常に〔オ〕>〔カ〕だから,値a1,a2,・・・,anの中に2が4個以上あれば,「2,2,2」を「3,3」に変えた方が
和Tnは大きくなる。
(キ) (a1,a2,・・・,an-2,1,1)
(ク) (a1,a2,・・・,an-2,2)
このとき,
〔キ〕=T n-2+A n-2+A n-2
〔ク〕=T n-2+2A n-2
だから, 〔キ〕=〔ク〕
よって,値a1,a2,・・・,anの中に1が2個以上あれば,「1,1」を「2」に変えても値Tnは変わらないので,
1が1個または0個の場合のみ考えればよい。
以上より,Tnの最大値となる条件は,
値a1,a2,・・・,anは,大きい方から順に並べたものであり,
すべて3以下の数で,2は3個以下,1は1個以下
である。
これを満たす値a1,a2,・・・,anを求めると,2008=3×669+1だから,
(ⅰ) 3,3,3,3,・・・,3,3,3,1
(ⅱ) 3,3,3,3,・・・,3,3,2,2
(ⅲ) 3,3,3,3,・・・,3,2,2,2,1
のいずれかである。ただし,赤い3は667個ある。
668項以降の積和を調べると,
(ⅰ) 3+9+9=21
(ⅱ) 3+6+12=21
(ⅲ) 2+4+8+8=22
だから,(ⅲ)が最大である。最大値は,
(3+32+33+・・・+3667)+3667×22