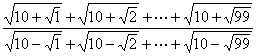200�X�N�@���{���w�I�����s�b�N�\�I�@���Ɖ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@2009�N1��12���@��������3����
|
�@�P�D�@�@���̐���n��p����n2�{�Sn�ƕ\���鐔�̂����C10000�Ƃ̍��̐�Βl���ł����������̂� �@�@�@���߂�B |
[�l����]�@
n�ɁC100�ɋ߂����������Ē��ׂ܂��B
[��]�@
P�in�j��n2�{�Sn��n�in�{�S�j�Ƃ����B
P�in�j�͑������ŁC�@�@P�i98�j��98�~102��9996�@������������đ������
P�i99�j��99�~103��10197
10000�Ƃ̍��̐�Βl������������P�i98�j�ł���B
�i���j�@9996�@��98�Ə����Ȃ��悤�ɒ��ӁI�I
|
�@�Q�D�@�@���a�Q�̉~�n1�Ɣ��a�S�̉~�n2���_�o�ŊO�ڂ��Ă���B�n1�C�n2�̎���ɂo�ƈقȂ�_�`�C�a �@�@�@�����ꂼ��Ƃ����Ƃ���C�`�C�o�C�a���꒼����ɕ���ł����B�����`�a�̒������S�ł���Ƃ��C �@�@�@�����o�a�̒��������߂�B �@�@�@ �@�@�@ |
[�l����]�@
�Q�̉~�̒��S������ŎO�p�`������܂��B
[��]�@
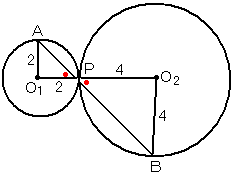
�}�ŁC���n1�`�o�䁢�n2�a�o������C�`�o�F�a�o���P�F�Q
![]()
![]()
|
�@�R�D�@�@���̂Q�̎����݂������̐����̑g�ia�Cb�Cc�j�����ׂċ��߂�B�������C�R�̐��̕��� �@�@�@���Ԃ��قȂ�g�͋�ʂ���B �@�@�@�@�@�@�@�@�@ab�{c��13 �@�@�@�@�@�@�@�@�@a�{bc��23 |
[�l����]�@
��̎����牺�̎��������ƁC���ӂ����������ł��鎮���ł��܂��B
[��]�@
ab�{c��13�@�E�E�E�i�A�j
a�{bc��23�@�E�E�E�i�C�j
�i�A�j�|�i�C�j���C
�@�@�@�@�@�@�@�@�@�@�@�@�@ab�{c�|a�|bc���|10 ���������́C��̈����Z����Ƃ���
�@�@�@�@�@�@�@�@�@b ( a�|c )�|( a�|c )���|10
�@ (a�|c ) (b�|1)���|10�@�E�E�E�i�E�j
b�|1�͐���10�̖�����C�@b�|1��1�C2�C5�C10�@������ł������܂���
�@�@�@�@�@�@�@�@�@b��2�C3�C6�C11
�i�A�j�C�i�E�j���C
b��2�̂Ƃ��C�@�����Ƃ͏��ɒ��ׂ邾���B
�@�@�@2a�{c��13
�@�@�@a�|c���|10�@�@�@����āCa���P�C c��11
b��3�̂Ƃ��C�@
�@�@�@3a�{c��13
�@�@�@ a�|c���|5�@�@�@����āCa��2�C c��7
b��6�̂Ƃ��C�@
�@�@�@6a�{c��13
�@�@ �@a�|c���|2�@�@�@a�Cc�������ɂȂ炸�s�K�B
b��11�̂Ƃ��C�@
�@�@�@11a�{c��13
�@�@�@ a�|c���|1�@�@�@����āCa��1�C c��2
�i���j �ia�Cb�Cc�j���i1�C2�C11�j�C�i2�C3�C7�j�C�i1�C11�C2�j
|
�@�S�D�@�@�O�p�`�`�a�b������C�ӂa�b�̒��_���l�Ƃ���ƁC�`�a���S�C�`�l���P�ł���B���̂Ƃ��C �@�@�@�ڂa�`�b�̑傫���Ƃ��Ă��肤��ŏ��̒l�����߂�B �@�@�@�@�������C�w�x�Ő����w�x�̒�����\�����̂Ƃ���B |
[�l����]�@
�u�����藝�v���g����`�ł����C�����H�v���Čv�Z�����炵�܂��B
[��]�@
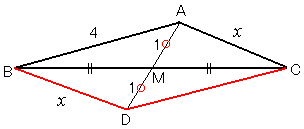
�}�̂悤�ɂc���Ƃ�B����������������Ƃ肠�����L���Ă݂�
�l�p�`�`�a�c�b�͕��s�l�ӌ`������C�ڂa�`�b��180���|�ڂ`�a�c
����āC�ڂ`�a�c���ő�ɂȂ�ꍇ���l����悢�B�����̕������������Ȃ��Ă���
���`�a�c�ŗ]���藝���g���āC
�@�@�@�@�@�@�@![]()
�����ŁC�i�������ρj���i���敽�ρj���g���ƁC�@�@
�@�@�@�@�@�@�@![]() �@
�@
������C�@�@
�@�@�@�@�@�@�@![]()
�ڂ`�a�c���ő�ɂȂ�̂́C
![]()
�܂�ڂ`�a�c��30���̂Ƃ��B
���̂Ƃ��C�ڂa�`�b��150��
�i���j150��
|
�@�T�D�@�@�Ԃ��ʂU�C���ʂR�C���F���ʂR�����ɕ��ׂ�B�ׂ肠���ǂ̂Q�̋ʂ��قȂ�F �@�@�@�ł���悤�ȕ��ו��͉��ʂ肠�邩�B�������C�����F�̋ʂ͋�ʂ��Ȃ����̂Ƃ���B �@�@�@ |
[�l����]�@
�܂����̑����Ԃ���ׂĂ����C���̊Ԃɐ�������ׂĂ����܂��B
[��]�@
�`�@���@�a�@���@�b�@�ԁ@�c�@���@�d�@���@�e�@���@�f
�Ƃ��āC�`�`�f�ɐ܂��͉��̋ʂ�u���B���a�C�b�C�c�C�d�C�e�ɂ͕K���ʂ�u��
�i�A�j�`�ɋʂ�u���ꍇ�@���[�ɒu�����u���Ȃ����ŏꍇ����������
�@�@�`�`�e�ɂ��ꂼ��P���ʂ�u�����ƂɂȂ�B���̕��@�́C
�@�@�@�@�@�@![]()
�i�C�j�f�ɋʂ�u���ꍇ
�@�@�i�A�j�Ɠ��l�ɁC 20�i�ʂ�j
�i�E�j�`�C�f�ɋʂ�u���Ȃ��ꍇ
�@�@�a�`�e�̂ǂ����P�ӏ��ɐƉ���u���̂ŁC���̕��@��10�ʂ�B
�@�c��̂S�ӏ��ɐ����P���u�����@�́C�@
�@�@�@�@�@�@![]()
����āC�ʂ̒u�����́C10�~6��60�i�ʂ�j
�i�A�j�`�i�E�j�������āC�P�O�O�ʂ�B
�i���j�P�O�O�ʂ�
|
�@�U�D�@�l�ʑ̂n�`�a�b�͂n�`���R�C�n�a���S�C�n�b���T����сڂ`�n�a���ڂ`�n�b���S�T���C�ڂa�n�b���U�O�� �@�@�@���݂����B���̂Ƃ��l�ʑ̂n�`�a�b�̑̐ς����߂�B �@�@�@�@�������C�w�x�Ő����w�x�̒�����\�����̂Ƃ���B |
[�l����]�@
�������S�T���̊p��Ώ̂Ȉʒu�ɒu���̂��R�c�ł��B���n�a�b���ʂɌ��܂��傤�B
[��]�@
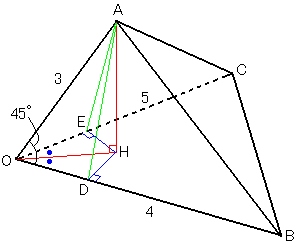
�}�̂悤�ɂg�C�c�C�d���Ƃ�ƁC
�`�c�ۂn�a�C�`�d�ۂn�b�@���u�R�����̒藝�v�B�n�a�ۂ`�g�C�n�a�ۂc�g�Ȃ̂ŁC�n�a�ۖʂ`�c�g�@����Ă`�c�ۂn�a��������B
���`�n�c�߁��`�n�d������C�`�c���`�d
����āC���`�c�g�߁��`�d�g�ƂȂ�C�c�g���d�g�ɂ��C���n�c�g�߁��n�d�g�ƂȂ�B���S�������ƂȂ�B
�@�@�@![]()
�@�@�@
�l�ʑ̂n�`�a�b�̑̐ς́C
�@�@![]()
�i���j�@�T
|
�@�V�D�@����x1�Cx2�Cx3�Cx4�Cx5�����̂T�̎����݂����B �@�@�@�@�@�@�@�@�@x1 x2�{x1 x3�{x1 x4�{x1 x5���|�P �@�@�@�@�@�@�@�@�@x2 x1�{x2 x3�{x2 x4�{x2 x5���|�P �@�@�@�@�@�@�@�@�@x3 x1�{x3 x2�{x3 x4�{x3 x5���|�P �@�@�@�@�@�@�@�@�@x4 x1�{x4 x2�{x4 x3�{x4 x5���|�P �@�@�@�@�@�@�@�@�@x5 x1�{x5 x2�{x5 x3�{x5 x4���|�P �@�@���̂Ƃ��Cx1�Ƃ��Ă��肤��l�����ׂċ��߂�B |
[�l����]�@
�܂��㉺�������Z���āC���ӂ������������ꂽ��������܂��B�^����ꂽ�����͂ǂ̕����ɂ��Ă�
�Ώ̂Ȃ̂ŁC���肤��l�Ƃ����̂͂ǂ̕����ɂ��Ă��������Ƃ������܂��B�������Œ肹���ɁC�Ȃ�ׂ�
��ʓI�ɑΏ̓I�ɍl����Ƃ߂�ǂ������Ȃ�Ȃ��悤�ł��B
[��]�@
�����͂ǂ̕����ɂ��Ă��Ώ̂�����C�P�̓��������藧�Ƃ��C���̎��̕��������ɓ���ւ���
���������藧�B�܂��ǂ̕����ɂ��Ă��Ƃ蓾��l�͓���������Cx1�����łȂ����ׂĂ̕����ɂ��āC
���̂Ƃ蓾��l�ׂ�B�����̂ق����l���₷���̂ŁB
��P���|��Q������C�@
�@�@�@�ix1�|x2�@�j�ix3�{x4�{x5�@�j���O�@�E�E�E�i�A�j
���̎��̔ԍ������ɉ�]�������C�Ⴆ�ix2�|x3�@�j�i�@x1�{x4�{x5�@�j���O�ȂǁC���ׂĐ��藧���Ă���B
�܂��C�T�̕������ǂ���قȂ�Ƃ���B�@�����������ꍇ���������Ƃ������Ă���
�i�A�j����C�@x3�{x4�{x5�@���O
��P���́@x1 x2�{x1 �ix3�{x4�{x5�j���|�P������Cx1 x2���|�P�@
���̂Q�����̐ς����ׂā|�P�ƂȂ�̂ŁC���Ώ̐��𗘗p
x1 x2�x2 x3�x3 x4�x4 x5�x5 x1���|�P�@
( x1 x2 x3 x4 x5 )2 ���|�P���O�ƂȂ�̂ŕs�K�B
����āC�T�̕����̂����ǂꂩ�͓������B
�����ŁCx1��x2��t �Ƃ��Ĉ�ʐ�������Ȃ��B���T�̕����S���̂Ƃ蓾��l���l���Ă���̂ŁC�����ݒ肵�Ă悢�B
t���O���Ƒ�P�������藧���Ȃ��̂ŁCt���O
�i�A�j�̕��������ւ��āC�@
�ix1�|x3�@�j�ix2�{x4�{x5�@�j���O���C
�@�@�@�@�@�@�@�@�@�@�i x3�|t�@�j�ix4�{x5�@�{t�@�j���O�@�E�E�E�i�C�j
���l�ɁC�@�@�@�i x4�|t�@�j�ix3�{x5�@�{t�@�j���O�@�E�E�E�i�E�j
�@ �i x5�|t�@�j�ix3�{x4�@�{t�@�j���O�@�E�E�E�i�G�j
�ix3�|x4�@�j�ix1�{x2�{x5�@�j���O���C
�@�@�@�@�@�@�@�@�@�@�@�ix3�|x4�@�j�i�Qt�{x5�@�j���O�@�E�E�E�i�I�j
�@�@���l�ɁC�@�@�@�@�ix3�|x5�@�j�i�Qt�{x4�@�j���O�@�E�E�E�i�J�j
�@�@�@ �@ �ix4�|x5�@�j�i�Qt�{x3�@�j���O�@�E�E�E�i�L�j
�@�@
�i�@�j�@x3�Cx4�Cx5�̂����ꂩ�� t�@�ɓ������Ƃ��C���ꍇ�������s��
�@�@�@x3��t �Ƃ��Ĉ�ʐ�������Ȃ��B
�@
���̂Ƃ��C�i�L�j���C�@�ix4�|x5�@�j�~�Rt���O�@�@t���O���Cx4��x5
�@�@�@x4��t �Ƃ����x1�`x5�����ׂ�t�ƂȂ�C��P���͂St2 ���|�P�ƂȂ�̂ŕs�K�B
�@�@�����x4��t�@������i�I�j���C�@x5���|�Qt
�i�A�j�@x3�Cx4�Cx5�̂������ t�@�ɓ������Ȃ��Ƃ��C���ꍇ�������s��
�@�@�@�i�C�j�`�i�G�j���C
�@�@�@�@�@�@�@�@x4�{x5�@���|t�@�Cx3�{x5�@���|t�@�Cx3�{x4�@���|t
�@�@�@����������āC
�@�@�@�@�@�@�@![]() �@
�@
�i�@�j�C(�A)�̂�����̏ꍇ�� x1�`x5 �́C���s���ŁC
�@�@�@�@�@�@�@s�@�Cs�@�Cs�@�C�|�Qs�C�|�Qs�@�@�����̂悤�ɂ܂Ƃ߂čl���邱�Ƃ��ł���
�ƕ\�����B
x1��s �Ƃ��đ�P���ɑ������ƁC�@�����̏ꍇ�����l����C����������o����B
�@�@�@�@s�i�@s�{s�|�Qs�|�Qs�@�j���|�P
�@�@�@�@�@�@�@![]() �@�@
�@�@
x1�̂Ƃ蓾��l�� s�@�܂��́|�Qs ������C
�@�@�@�@�@�@![]()
![]()
|
�@�W�D�@f (x)�Cg (x)�͂�������������W���Ƃ���O�łȂ��������ŁC �@�@�@�@�@f ( x3 )�{g (x) �� f ( x )�{x5 g (x) ���݂����B���̂悤��f (x)�Ƃ��Ă��肤����̂̂����C�������ł����������̂��P���߂�B |
[�l����]�@
�@f ( x3 )�|f ( x )���ix5 �|�P�jg (x)�@������C���ӂ̎���x5 �|�P�Ŋ����邱�ƂɂȂ�܂��B�Ȃ̂ŏ��H
��������f ( x )�����Œu���āC���ۂ�x5 �|�P�Ŋ����Ă݂܂��傤�B
[��]�@
f ( x3 )�|f ( x )���ix5 �|�P�jg (x)�@������Cf ( x3 )�|f ( x )��x5 �|�P�Ŋ�����B
�܂��@f ( x )��ax3�{bx2�{cx�{d�Ƃ����ƁC�@��a��0�ł��n�j�B����ʼn���������S���ȏ�ׂȂ��čςށB
�@�@�@�@f ( x3 )��ax9�{bx6�{cx3�{d
������C
�@�@f ( x3 )�|f ( x )��ax9�{bx6�{�ic�|a�jx3�|bx2�|cx
��x�o a x8�{bx5�{�ic�|a�jx2�|bx�|c �p�@��x��������o������
�o�@�@�p����x5 �|�P�Ŋ���ƁC
������C���́@a x3�{b
�@�@�@�@�@�]��́@a x3�{�ic�|a�jx2�|bx�{b�|c
�]�肪0�ɂȂ�̂ŁCa��c�|a���|b��b�|c��0�@���W����S��0�Ƃ���
�����a��b��c��0������Cf ( x3 )�|f ( x )��0�ƂȂ�Cg (x)�@��0�ƂȂ�̂ŕs�K�B
������f ( x )�͂S���ȏ�̎��ł���B
�@f ( x )��ex4�{�iax3�{bx2�{cx�{d )�@�Ƃ����ƁC����̊���Z�̌��ʂ��g�������̂ŁC���������B
f ( x3 )��ex12�{�iax9�{bx6�{cx3�{d )�@ �@�@�@�@���S���ʼn����������Ăق����Ɗ��҂��E�E
������C
�@�@f ( x3 )�|f ( x )��ex12�|ex4�{x�ia x8�{bx5�{�ic�|a�jx2�|bx�|c�j
�ό`����ƁC��x5 �|�P�Ŋ������`�̎�������̂��ڕW
�@�@f ( x3 )�|f ( x )��e�ix5 �|�P�j�ix7�{x2�j�|ex4�{ex2�{�@x�ix5 �|�P�j�ia x3�{b�j�{a x4�{�ic�|a�jx3�|bx2�{�ib�|c�jx
�@�@�@�@�@�@�@�@�@�@���ix5 �|�P�j�ie x7�{e x2�{a x4�{bx�j�{�ia�|e�jx4�{�ic�|a�jx3�{�ie�|b�jx2�{�ib�|c�jx
x5 �|�P�Ŋ������]��́C
�@�@�@�@�@�ia�|e�jx4�{�ic�|a�jx3�{�ie�|b�jx2�{�ib�|c�jx
���ꂪ0�ɂȂ�̂ŁC a�|e��c�|a��e�|b��b�|c��0
����āC�@a��b��c��e
�@�@�@�@�@f ( x )��a x4�{ax3�{ax2�{ax�{d�@�����ꂪ��ʌ`�B
�i���j�@f ( x )��x4�{x3�{x2�{x�@�@���P���������
|
�@�X�D�@���鐔�w�̍��ۑ��ɂP�O�l�̒ʖ��҂��ꂽ�B�e�ʖ�́C�M���V����C�X���x�j�A��C �@�@�@�x�g�i����C�X�y�C����C�h�C�c��̂������傤�ǂQ��b�����Ƃ��ł���B�܂��C�ǂ̂Q�l�ɂ� �@�@�@�Ă��C�b���錾��̑g�ݍ��킹�͈قȂ�B �@�@�@���̒ʖ����Q�l���T�̕����ɏh�������邱�ƂɂȂ����B�ǂ̕����ɏh������Q�l������ �@�@�@�̌����b����悤�ȕ�������ɂ������B���̂悤�ȕ��@�͉��ʂ肠�邩�B �@�@�@�������C������ւ��������Ől�̑g�ݍ��킹���S��������������́C����̂��̂Ƃ��Đ�����B�@�@ |
[�l����]�@
���܂����������l���Ȃ��ƁC�Ƃ�ł��Ȃ��ʓ|�ɂȂ�܂��B�P�p�^�[�����ׂĂ�������{���������̂������C
�Ƃ����ӂ��ɉ�����悤�ɂ��܂��B
[��]�@
�T�̌�������ɂ`�C�a�C�b�C�c�C�d�Ƃ��āC�P�O�l�̒ʖ���C
�`�a�C�`�b�C�`�c�C�`�d�C�a�b�C�a�c�C�a�d�C�b�c�C�b�d�C�c�d
�ƕ\���B
�`�a�ƃy�A�ɂȂ肤��l�͂`�b�C�`�c�C�`�d�C�a�b�C�a�c�C�a�d�̂U�l�ŁC���ꂼ��̏ꍇ�̕�������ɏd���͂Ȃ��C
��������̑����͓����ł���B������C
�@�@�`�a�Ƃ`�b���y�A�ɂȂ�Ƃ��̕�������̐������߁C������U�{���������@�@���P���Œ肳����l����
�������ƂȂ�B
�`�a�Ƃ`�b���y�A�ɂȂ�ꍇ�ɂ����āC�`��b����ʖ�`�c�C�`�d���y�A�������łȂ����ŏꍇ��������B
�i�@�j�@�`�c�C�`�d���y�A�ł���Ƃ�
�@�c��̂U�l�a�b�C�a�c�C�a�d�C�b�c�C�b�d�C�c�d�łR�̃y�A������B
�@�����ŁC���ʂȌ���ɂȂ肤�錾��͂a�C�b�C�c�C�d����I�R������C���ǂ̌���Ńy�A�ɂȂ邩���l����
�@���ʂȌ���̑I�ѕ��͂S�ʂ�B
�@���̂����C���ʂȌ��ꂪ�a�C�b�C�c�̂Ƃ��́C���d�����l�́C��������̌���Ńy�A�ɂȂ邵���Ȃ�
�@�@�@�@�E�i�a�b�C�a�d�j�C�i�b�c�C�b�d�j�C�i�a�c�C�c�d�j
�@�@�@�@�E�i�a�c�C�a�d�j�C�i�a�b�C�b�d�j�C�i�b�c�C�c�d�j
�@�̂Q�ʂ肠��B
�@����āC�i�@�j�̏ꍇ�̕�������̐��́C�S�~�Q���W�i�ʂ�j
�i�A�j�@�`�c�C�`�d���y�A�łȂ��Ƃ�
�@�`�c�ƃy�A�ɂȂ肤��l�́C�a�c�C�b�c�C�c�d�̂R�l�C
�@�`�d�ƃy�A�ɂȂ肤��l�́C�a�d�C�b�d�C�c�d�̂R�l�ŁC���̂Q�̃y�A�̂�����́C
�@�@�@�R�~�R�|�P���W�i�ʂ�j�@���i�`�c�C�c�d�j���i�`�d�C�c�d�j�Ƃ����ꍇ������
�@���̂����i�`�c�C�a�c�j���i�`�d�C�a�d�j�̂Ƃ��́C�c��̃y�A�̕��@��
�@�@�@�@�@�@�E�i�a�b�C�b�c�j�C�i�b�d�C�c�d�j
�@�@�@�@�@�@�E�i�a�b�C�b�d�j�C�i�b�c�C�c�d�j
�@�̂Q�ʂ肠��B���ق��̏ꍇ�������Q�ʂ肠��
�@����āC�i�A�j�̏ꍇ�̕�������̐��́C�W�~�Q���P�U�i�ʂ�j
(�@)�C�i�A�j���C�@�`�a�Ƃ`�b���y�A�ɂȂ�ꍇ�̕�������̐��́C�W�{�P�U���Q�S�i�ʂ�j
����āC�S�̂̕�������̐��́C�Q�S�~�U���P�S�S�i�ʂ�j
�i���j�@�P�S�S�ʂ�
|
�@�P�O�D�@�ȉ����v�Z����B �@�@�@�@�@�@ �@�@�@�������C����� �@�@�@ |
[�l����]�@
�Q�d�������͂������Ƃ͖��������C���q�ƕ�������ꂼ��v�Z���邱�Ƃ������ł��B�H�v���K�v�B
���q�̘a��S�C����̘a��T�Ƃ����āCS�� T�̊W��������Ƃ������z�ł����܂��B
[��]�@
���q�̘a��S�C����̘a��T�Ƃ���B
���܁Cn�����R���Ƃ��āC
![]() �@�i��0�j�@�@
�@�i��0�j�@�@
�̒l���l����B��n�ɂP�`99�܂ő�����ĉ������S�{T�ƂȂ�B
�@�@![]()
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@![]()
������C�@![]()
n���P�`99�Ƃ��āC99�̎������ׂĉ�����ƁC���E�ӂ�S���t�]���Č����
�@�@�@![]()
�@�@�@![]()
�@�@�@![]()
![]()
|
�@�P�P�D�@����x�ɂ��Ă̕����� �@�@�@�@�@[ x ]�{[ 2x ]�{[ 3x ]�{[ 4x ]�{[ 5x ]�{[ 6x ]�{[ 7x ]�{[ 8x ]�{[ 9x ]��44x �̉��̑��a�����߂�B �@�@�@�������C����r�ɑ���r���Ȃ��ő�̐�����[r ]�ŕ\���B |
[�l����]�@
���ӂ͐����Ȃ̂ʼnE�ӂ������ƂȂ�܂��B44x�������Ƃ������ƂŁC�Ƃ肠����x�́u���ꂪ�S�S�̗L�����v
�Ƃ������Ƃ��킩��܂��B���̂��Ƃ�����E�E�B
[��]�@
�@[ x ]�{[ 2x ]�{[ 3x ]�{[ 4x ]�{[ 5x ]�{[ 6x ]�{[ 7x ]�{[ 8x ]�{[ 9x ]��44x�@�E�E�E�i���j
���ӂ͐���������C�E��44x�������ł���C����ɂ���
x �́C
![]() �@
�@
�ƕ\����B�������CN ( k )�͐����ŁCk ��0�C1�C2�C�E�E�E�C43
k ��0�̂Ƃ��Cx�͐���������C�i���j�́C
�@�@x �{2x �{ 3x �{ 4x �{ 5x �{ 6x �{ 7x �{ 8x �{ 9x ��44x
�@�@45x ��44x
x ��0
���̘a�����߂�̂ł���͖������Ă悢�B�ȉ��Ck ��1�C2�C�E�E�E�C43 �̏ꍇ���l����B
�i���j�ɉ� x ��������ƁC
�@�@�@�@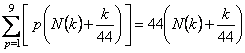
�@�@�@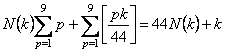
�@�@�@�@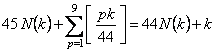
�@�@�@�@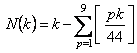
����āC�i���j�̉��́C
�@�@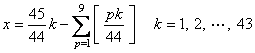
�����Ƃ́C�����S�������������ƂɂȂ�܂��B
�i���j�̉��̘a
T �́C
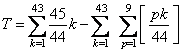
�@�@ 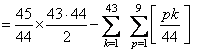
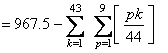
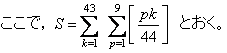
������S�����߂邽�߂Ɉȉ��H�v�����̂ł����C���܂胉�N�ɂȂ��ĂȂ��E�E
![]()
![]()
![]()
![]()
�@�@�@�@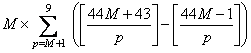
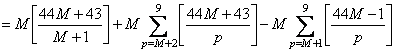
�@�@�@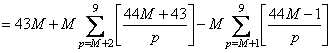
�@�@�@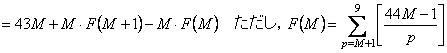
�@�@�@��43M�|F�iM�{�P�j�{�o�iM�{�P�j�EF�iM�{�P�j�|M�EF�iM�j�p�@�������Ə�����`��������B
���̎��� F(9)��0 �Ƃ���� M��1�C2�C�E�E�E�C8 �Ő��藧�B
M�@��1�C2�C�E�E�E�C8�Ƃ��Ă��ׂĉ�����ƁC
�@�@�@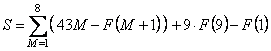
�@�@�@�@![]()
�@�@�@�@![]()
���Ƃ� F (1)�`F (8) �����߂�Γ������o����B������ƃe���p�������E�E�B
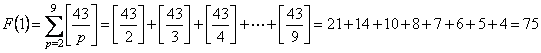
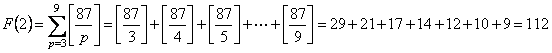
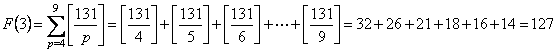
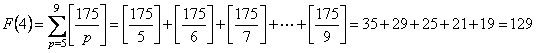
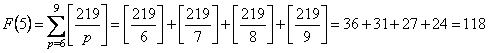
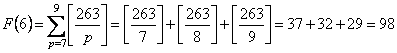
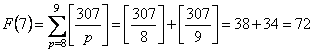
����āC
S��1548�|�i75�{112�{127�{129�{118�{98�{72�{39�j
��1548�|770
��778
T��967.5�|778��189.5
�i���j�@189.5
|
�@�P�Q�D�@��Ԃ͂��̒��̕��ʂɂ���ĂQ�̕����ɕ�����邪�C���̂�������i���ʂ͊܂܂Ȃ��j �@�@�@�@��ԂƂ����BS ���C�ǂ̂S�_�����ꕽ�ʏ�ɂȂ��悤�ȋ�ԓ��̂P�O�_����Ȃ�W���Ƃ���B �@�@�@�@���̂Ƃ��CS �̕����W���ł����āCS�Ƃ��锼��Ԃ̋��ʕ����ƂȂ���̂̌������߂�B |
[�l����]�@
��Ԃ��P�̕��ʂŐ��ĂQ�̕����ɕ������Ƃ��C���̕Е��̕����ɓ����Ă���_���P�̏W�����݂āC
���������W�������ł��邩�����߂�悢�킯�ł��B�ł����C�P�O�̓_���ǂ�Ȉʒu�ɂ��邩�Ő�����
���ς���Ă��܂��C��₱�����E�E�B�P�O�̓_�œʂȑ��ʑ̂��ł���ꍇ�́C���Ƃ�������ꂻ���ł��B
�L�q���łȂ��������������������Ȃ̂ŁC�ʂȑ��ʑ̂�`���Đ����C������ɂ��Ă����Ǝv���܂��B
[�P]�@�i�����ȉł͂���܂���B�j
10�̓_�����ԂƓʑ��ʑ̂��ł���ꍇ�B
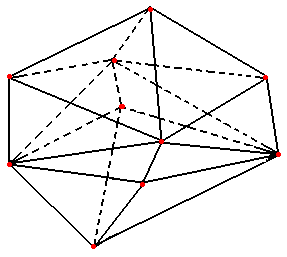
���̓ʑ��ʑ̂́C���_�̐�10�C�ʂ̐�16�C�ӂ̐�24�ł���B
�i�A�j�����W���̗v�f���P�_�����̂Ƃ��@���P�_�Őڂ��镽�ʂ��C�������炵�����ʂ��l����
�@�@����͕��ʂ��P�_���������ꍇ�ł���B���̂悤�ȕ��ʂ�
�@�@���_�̌������l������̂ŁC10�B
�i�C�j�����W���̗v�f���Q�_�����̂Ƃ��@��1�{�̕ӂŐڂ��镽�ʂ��C�������炵�����ʂ��l����
�@�@����͕��ʂ��Q�_���������ꍇ�ł���B���̂悤�ȕ��ʂ�
�@�@�ӂ̖{�������l������̂ŁC24�B
�i�E�j��L�ȊO�̏ꍇ�@���O���R�_�ȏ�܂܂��ꍇ
�@�@S�̕����W���̂����C��W���ƑS�̏W���͏������݂����B�����2�B
�@���ɁC
�@���ʑ̂̂R�̒��_��ʂ镽�ʃ��l���C���̕��ʂɂ����锼��Ԃ�U�Ƃ���B
�@���܁C�@�@T ���o�@�_X �bX �́CU�܂��̓ɂ���_ �p
�@�Ƃ���ƁC�W��T�́C���ʃs�ړ��������ʂɂ���đ�ӂ��݂��������W���Ƃ��邱�Ƃ��ł���B
�@���̂悤��T�̑����́C10C3�~2�@�ʂ�B�@��T�͗��T�C�h�ɂ���̂ŁC�Q�{����B
�@���������ʃ��ʑ��ʑ̖̂ʂƈ�v����Ƃ��C�W��T���S�̏W���ƈ�v����ꍇ���o�Ă���̂ŁC
�@����������ƁC
�@�@�@�@�@�@![]()
�@������C�i�E�j�̏ꍇ�̐��́C226�ʂ�B
�i�A�j�`�i�E�j�����ׂđ����ƁC�@10�{24�{226��260�i�ʂ�j
�i���j�@260��
[�Q]�@�i���Ԃ����Ǝv���܂����C���M�Ȃ��j
n �̓_�ɂ��āC�������������W���̌���
f ( n ) �Ƃ���B
���܁C f ( 1 )��2�@�@(��W�����S�̏W����2��)
f ( 2 )��4�@�@(�v�f�̌���0��1��2��4��)
f ( 3 )�́C�v�f�̌���0��1��2��3�̏ꍇ�����v���āC
�@�@ �@f ( 3 )��1�{3�{3�{1��8�@�������܂ł͕��ꂪ������������
n��3�̂Ƃ��Cf ( n ) �̑Q����������B
n�{1�̓_������Ƃ��C
�P�̕��ʏ�ɂ��̂����̂P�_�o���C�c���n �̓_�����ׂĔ���Ԃɂ���悤�ɂł���B
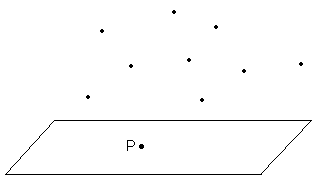
����f ( n�{1 )�𐔂���Ƃ��C
�o���̂���n�̓_�ł͕����W����f ( n )�����ł��邪�C����f ( n )�̏W���ɂ͂o���܂܂�Ă��Ȃ��B
n�{1�̓_�ōl�����f ( n )�̏W���̒��ɂ͗v�f�ɂo���܂ނ��̂����������݂���B�����悻��������
���C���̏W�����J�E���g�������Ƃɂ��C����ȊO�̏W���ׂ�B����������₱�����ł��ˁE�E�B
�܂��C�o�Ƒ��̂Q�_�`�C�a��ʂ镽�ʃ��l���C���̕��ʂɂ����锼��Ԃ�U�Ƃ���B
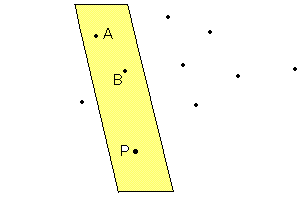
���܁C�@�@T ���o�@�_X �bX �́CU�̓_�܂��͂`�C�a�C�o �p
�Ƃ���ƁC�W��T�́C���ʃs�ړ��������ʂɂ���đ�ӂ��݂��������W���Ƃ��邱�Ƃ��ł���B
���̂悤��T�̑����́C ��T�͗��T�C�h�ɂ���̂ŁC�Q�{����B
![]()
�܂��C��W���ƂP�_�o�݂̂̏W���͏������݂����B����2�������āCn2�|n�{2�B
f ( n�{1 )�����߂�ہC���́in2�|n�{2�j�̏W���ɂ���āC
�@�@��W���C�P�_�o�݂̂̏W���C�o���܂ނR�_�ȏ�̗v�f����Ȃ�W��
�����ׂĐ�����ꂽ���ƂɂȂ�B���S�̏W�����J�E���g����Ă���
����ȊO�̏W�����l����ƁC
�@�@�o�Ƃ��ƂP�_�݂̗̂v�f����Ȃ�W���C�o���܂܂Ȃ���łȂ��W��
�����邪�C������f ( n ) �̒��ɂ��łɃJ�E���g����Ă���B���킩��ɂ����E�E
�܂��C��ɐ�����f ( n ) �̏W���ƁC���Ƃ́in2�|n�{2�j�̏W���ɂ͏d�����Ȃ��B���킩��ɂ����E�E
����āC�@f ( n�{1 )��f ( n )�{n2�|n�{2�@���Q�����������I�I
���̎���n��1�C2�C3�C�E�E�E�Ő��藧�B
�@�@�@�@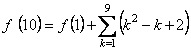
�@�@�@�@�@�@�@�@![]()
�@�@�@�@�@�@�@�@��2�{285�|45�{18
��260�@�@
�i���j260��