2008�N�@���{���w�I�����s�b�N�{�I�@���Ɖ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�Q�O�O�W�N�@�Q���P�P���@�������ԂS����
|
�@�P�D�@�����W��������P ( x )�́C����0�łȂ�����n�ɂ���P (n2 )��0�����B���̂Ƃ��C �@�@�@0�łȂ��C�ӂ̗L����a�ɑ���P (a2 )��1�ł��邱�Ƃ������B |
[�l����]
P (a2 )��1�ƂȂ�L����a�����݂����Ƃ��āC�������܂��B
[��]
P (n2 )��0���CP ( x )��x�|n2�������ɂ��B����āC
�@�@�@�@P ( x )���ix�|n2�jQ ( x )
�ƕ\�����C�����ŁCQ ( x )�͐����W���̑������ł���B�Ȃ��Ȃ�C
P ( x )��m�����ŁCxk�̌W����bk�Ƃ���ƁC�g�����@���C
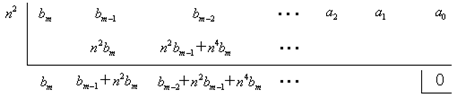
���Ɍ����m�|�P�̐���Q ( x )�̌W���ƂȂ邪�C�����͂��ׂĐ����ǂ����̐ς̘a�ł���̂ŁC
�݂Ȑ����ł���B
���ɁCP (a2 )��1�ƂȂ�L����a�����݂����Ɖ��肷��B�����_��ے肵�āC�������B
���̂Ƃ��C�ia2�|n2�jQ (a2 )��1�����藧�B���ӂ�0�łȂ��̂ŁCa2��n2�ł���B

���̓����̍��ӂ͐����ł���B���E�ӂ������ɂȂ�Ȃ����Ƃ������悢�B
���ɁCp��q�{|pn|�̍ő����d�i���P�j�Ƃ���B���̂Ƃ��Cp��dM�Cq�{|pn|= dN�Ƃ����ƁC
�@�@�@�@q���iq�{|pn|�j�||pn|��dN�||dM n|��d�iN�||Mn|�j�@��d���P�ɂȂ邱�Ƃ��Ă���B
������Cd��q�̖ł�����Bp�Cq�݂͌��ɑf������Cd���P
����āCp��q�{|pn|�݂͌��ɑf�ł���B�܂��Cq�{|pn|��q�{|p|���P������C���̉E�ӂł́Cp2m��q�{|pn|
�ƂŖ��N����Ȃ��B���Ȃ킿���̉E�ӂ͐����ł͂Ȃ��B
����͖����ł���B
����āC0�łȂ��C�ӂ̗L����a�ɑ���P (a2 )��1�ł���B�@�@(q.e.d)
|
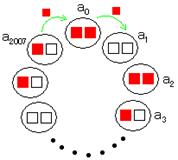
�@�Q�D�@�Ԃ��J�[�h�Ɣ����J�[�h�����ꂼ��2008��������B2008�l�̃v���C���[���C���ꂼ�� �@�@�@�����̃J�[�h�̂����Q�����z��ꂽ��ԂŁC�����������ĉ~�`�ɂȂ��č���B�P��̃^�[�� �@�@�@�őS���������Ɏ��̂��Ƃ��s���B �@�@�@�@�@�@�E�Ԃ��J�[�h���P���ł������Ă���ΐԂ��J�[�h1�������ׂ̃v���C���[�ɓn���B �@�@�@�@�@�@�@�Ԃ��J�[�h���P���������Ă��Ȃ���Δ����J�[�h1�������ׂ̃v���C���[�ɓn���B �@�@�@���̂Ƃ��C���߂đS�����Ԃ��J�[�h�Ɣ����J�[�h��1���������Ă����ԂɂȂ�܂łɂ����� �@�@�@�^�[�����̍ő�l�����߂�B �@�@�@ |
[�l����]�@
�ԂQ�������l�ƁC���Q�������l�̐l���͏�ɓ����ł��B�l�����������ė��l�߂ʼn������Ƃ����
�̂ŁC�܂����^�[�����̏���ׁC���ɂ��̒l�����肤�邱�Ƃ������C���̕��@�ōs���܂��B
[��]�@
�ԂQ�������l��A�C���Q�����l��B�C�Ԕ��P�������l��C�Ƃ���B
����^�[�����Ă��CA��B�̐l���͓����ł���C1��̃^�[���ł́C�Q�O�O�W���̃J�[�h�̈ړ��̂����CB��
�l���Ɠ��������̔����J�[�h�����C����ȊO�͂��ׂĐԂ��J�[�h�ł���B
�S�����Ԃ��J�[�h�Ɣ����J�[�h��1���������Ă����ԂƂ́C����^�[���̂̂��C�S�����Ԃ��J�[�h��
��Ɏ����Ƃł���B
�����ŁC�^�[�����Q�O�O�V��s���C�K���S����C�̏�ԂɂȂ邱�Ƃ������B���V����I�ł��ȁB
���܁C�^�[�����Q�O�O�V��s�������ʁC�`�ł������l�������Ƃ��āC���̐l��a0�Ƃ���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��a0�����Ȃ���C�S���b�ɂȂ��Ă���Ba0�����Ȃ����Ƃ�w���@�Ŏ����B
�����J�[�h������a�܂��͂b�̏�ԂɂȂ�̂ŁCa0�͂͂��߂���`�̏�Ԃł���C���ׂẴ^�[���ŐԂ�
�J�[�h�����Ă��邱�ƂɂȂ�B
|
�����ŁCa0�̍��ׂ�a1�Ƃ��Ca1�̍��ׂ�a2�Ƃ��C�ȉ����ɁC a3�Ca4�C�E�E�E�Ca2007�Ƃ���B �E�ׂ̐l���Ԃ��J�[�h�������Ă���ΕK���Ԃ����̂ŁC �@�@a1�́Ca0����K���Ԃ����炤�B �@�@a2�́Ca1����Q��ڂ̃^�[���ŐԂ����炢�C���̌シ�ׂĐԂ�����B �@�@a3�́Ca2����R��ڂ̃^�[���ŐԂ����炢�C���̌シ�ׂĐԂ�����B �@�@�@�@�E�E�E�E�E�E�E�@�@�@�@�@�@�@�@�@�����̂悤�ɂǂ�ǂ�Ԃ��肪����Ă���B �@�@a2007�́Ca2006����Q�O�O�V��ڂ̃^�[���ŐԂ����炤�B |
|
�ȏ���C�Q�O�O�V��ڂ̃^�[���ŁC�S�����Ԃ������ƂɂȂ邪�Ca0�͐Ԃ��Q�����L���Ă���̂ŁC�Ԃ̕�
������薇���������Ȃ��Ė�������B
����āC�^�[�����Q�O�O�V��s�����ꍇ�C�`�ł���l�͂��Ȃ��B�܂�C�S����C�̏�ԂɂȂ�B
���Ȃ킿�C�^�[���̍ő�l�͂Q�O�O�V�ȉ��ł���B
���ɁC�Q�O�O�V��̃^�[���őS����C�̏�ԂɂȂ�ꍇ�����邱�Ƃ������B
�`���P�O�O�S�l�C�a���P�O�O�S�l���āC�`�ǂ����ׂ荇���C�a�ǂ����ׂ荇�����ꍇ���l����ƁC�A���Q��̃^�[��
�ŁC�`�P�O�O�S�l�̉E�[�̂P�l���a�ƂȂ�B������J��Ԃ��ƁC�Q�~�P�O�O�R��̃^�[���Ō��̂`�P�O�O�S�l�̂����C
�P�O�O�R�l�ɔ����n��C���[�̐l�݂̂��`�ł���B���̃^�[���ł��̐l�ɂ������n��̂ŁC����őS����
C�̏�ԂƂȂ�B
�i���j�@�Q�O�O�V
|
�@�R�D�@�s�p�O�p�`ABC�̊O�S��O�Ƃ���B�Q�_A�CO��ʂ�~���C����AB�CAC�Ƃ��ꂼ�� �@�@�@A�ȊO�̓_P�CQ�Ō�����Ă���B����PQ�Ɛ���BC�̒������������Ƃ��C����PQ�� �@�@�@����BC�̂Ȃ��p�̂����X�O���ȉ��̕��̑傫�������߂�B |
[�l����]�@
BC��PQ����C���S�p�����������Ƃ��킩��܂��B
[��]�@
�Q�_A�CO��ʂ�~�̒��S��O'�Ƃ���B���}�̂悤�ɁCO'��AO�Ɋւ���C�̑��ɂ���Ƃ��Ă悢�B
�i�@�j�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�A�j
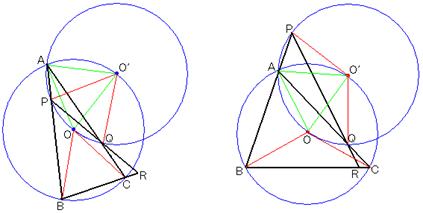
�~O'�̉~���p��PAQ�́C��PAQ����BAC �܂��́�PAQ���P�W�O���|��BAC�̂Q��ނ���B
BC��PQ������C������ɂ��Ă��C�~O�̗��BC�̉~���p�ƁC�~O'�̗��PQ�̉~���p�͓������B
����ɂ�肻�ꂼ��̒��S�p������������C�ӎO�p�`OBC��O'PQ�̒��p�͓������B
BC��PQ���C�����̒�ӂ�����������C��OBC�߁�O'PQ
����āC2�~�̔��a�͓������B�����̏������J�M�ł��ˁB
���Ȃ킿�C��AOO'�͐��O�p�`�ł���B
���ɁCPQ��BC�̌�_��R�Ƃ���B���߂�p�́�PRB�ł���B
�i�@�j�̂Ƃ��C��������ɋ��߂������C�������ۂ��B
��PRB����ACB�|��CQR���i��OCB�{��OCA�j�|��AQP
�@�@�@�@���i��O'QP�{��OAQ�j�|��AQP
�@�@�@�@���i��O'QP�|��AQP�j�{��OAQ
�@�@�@�@����O'QA�{��OAQ
�@�@�@�@����O'AQ�{��OAQ����OAO'���U�O��
�@�@�@�p���`�b�̉����ɂ���Ƃ����C�S�������Ɏ�����B
�i�A�j�̂Ƃ��C
��PRB����ACB�{��CQR���i��OCB�{��OCA�j�{��AQP
�@�@�@�@���i��O'QP�{��OAQ�j�{��AQP
�@�@�@�@���i��O'QP�{��AQP�j�{��OAQ
�@�@�@�@����O'QA�{��OAQ�@�@����������(�@)�Ɠ����B
�@�@�@�@����O'AQ�{��OAQ����OAO'���U�O��
�i���j�@�U�O��
|
�@�S�D�@�����ɑ��Ē�`����C�����l���Ƃ�� f �ł����āC�C�ӂ̎��� x�Cy �ɑ��āC �@�@�@�@�@�@�@�@�@�@�@�@f ( x�{y ) f ( f (x )�|y )��x f ( x )�|y f ( y )�@ �@�@�������̂����ׂċ��߂�B |
[�l����]�@
x��y��0�Ȃǂ������āC��������������画�f���܂��B�ǂ�Ȋ��������Ȃ̂����������Ȃ��B
f ( x )��0��f ( x )��x�́C���̓��������Ă��܂��B�i��̎����Ȋ��������ɂȂ�j�@�Ȃ̂ŁC������
�����Ȃ邱�Ƃ����z���ē����Ă����܂��B�ł�����ȊO�ɖ����������Ȃ����Ƃ������̂����Ȃ����B
[��]�@
�@
�@f ( x�{y ) f ( f (x )�|y )��x f ( x )�|y f ( y )�@�E�E�E�E�E�E�i���j
�i���j��y��0��������ƁC���܂��O�����B
f ( x ) f ( f (x ) )��x f ( x )
�@�@�@�@�@�@�@�@�@�@�@�@ f ( x ) �o f ( f (x ) )�|x �p��0
�i���j��x��0�Cy��x��������ƁC�@��������ɂ�����B
f ( x ) f ( f (0 )�|x )���|x f ( x )
f ( 0 )��t �Ƃ���ƁC�@�@f ( x ) �o f (t�|x ) )�{x �p��0
f ( x )��0 �Ȃ�����̓��������C�i���j���������̂ŁC����ȊO�̊����l����B
f ( x )��0�̂Ƃ��C
�@�@�@�@�@�@�@�@�@�@�@�@�@�@f ( f ( x ) )��x�@�@�E�E�E�E�E�E�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@f ( t�|x )���|x�@�E�E�E�E�E�E�A
������t��0��0�łȂ����ŏꍇ����������B�@���������Ȃ�.���C����������ƍl���₷���B
(�@)�@ f ( 0 )��t��0�̂Ƃ�
�@x��0�Ŋ� f ( x )���l����B
�@�A���Cf ( x )��0�̂Ƃ��C�@f (�|x )���|x�@�i��0�j�@�E�E�E�E�E�E�A�L
�@f (�|x )��0������C�A�L��x�Ɂ|x�������āC
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@f ( x )��x�@�@
����āCf ( x )��0�ƂȂ�x�ɑ��C
f ( x )��x�@�ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@������ŏI���ł͂Ȃ��Bf (x)��0�ƂȂ�ꍇ�����邩�C�ᖡ���K�v�B
�@���܁C�������f ( x )��0�ł͂Ȃ��ꍇ���l���Ă���̂ŁCf ( c )��0�ƂȂ�c�i��0�j�����݂��Ă���B
�@�����ŁCf ( d )��0�ƂȂ�d�i��0�j�����݂����Ƃ���B���Ɖ��肵�Ė������B
�i���j��x��c�Cy��d ��������ƁC
�@f ( c�{d ) f ( f (c )�|d )��c f ( c )�| d f ( d )�@
f ( c )��c�Cf ( d )��0������C f ( c�{d ) f ( c�|d )��c2 �E�E�E�E�E�E�B
c��0������C�@�@�@f ( c�{d )��0�C f ( c�|d )��0
�@����āC�@�@ �@�@f ( c�{d )��c�{d�C f ( c�|d )��c�|d�@�����܂����������B
�@�B�ɑ������ƁC�@�@�@�@�@( c�{d ) ( c�|d )��c2�@�@c2�|d 2��c2
d��0�ƂȂ�C����͖����ł���B
����āCx��0�̂Ƃ��Cf ( x )��0
�@�ȏ���C��
f ( x )�́C
�@�@�@�@�@�@�@�@�@�@�@�@�@f ( x )��x�@
�@���� f ( x )�͏�Ɂi���j�����B���������ΐ��藧���Ƃ��킩��B
(�A)�@ f ( 0 )��t��0�̂Ƃ�
�@f ( 0 )��0������C�A��
x��0�������C
f ( t )��0
�@�����ŁCf ( c )��0�ƂȂ� c�i��0�j�����݂����Ƃ���B�@���������肵�Ė������B
�@���̂Ƃ��Cc��0�Cc��t �ł���B�@��c��t�Ƃ����f (c)��f (t)��0�Ŗ����Ȃ̂ŁB
�@�A���C�@�@�@�@�@�@�@f ( t�|c )���|c �i��0�j�E�E�E�E�E�E�C
�@f ( t�|c )��0������C�@�� x��t�|c �������C�@����������������\�ɂȂ�B
f ( f ( t�|c ) )��t�|c
f (�|c )��t�|c�i��0�j
�@f (�|c )��0������C�A�� x���|c �������C�@�������������ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@f ( t�{c )��c�@�E�E�E�E�E�E�D
�@�i���j�� x��t�{c�Cy��t�|c ��������ƁC�@����J���āC���̑���������B
�@�@�@�@�@�@�@�@�@f ( 2t ) f ( f (t�{c )�|( t�|c ) )��( t�{c ) f (t�{c )�|( t�|c ) f (t�|c )
�B�C�C�������C
�@�@�@�@�@�@�@ f ( 2t ) f ( 2 c�|t )��( t�{c ) c�|( t�|c ) (�|c )
�@
f ( 2t ) f ( 2 c�|t )��2 c t
c t��0������C f ( 2t )��0 �E�E�E�E�E�E�E�@�����ꂪ�����̍ޗ��ɂȂ�B
�@�E���C�A��
x��2t �������C
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@f (�|t )���|2 t �i��0�j�E�E�E�E�E�E�F�@������������̍ޗ��ɂȂ�B
�@����Ɂi���j��
x��t�Cy��t ��������ƁC
f ( 2t ) f ( f ( t )�| t )��t f ( t )�|t f ( t )
�@�@�@�@�@�@�@�@�@�@f ( 2t ) f (�|t ) ��0 �E�E�E�E�E�E�G
�@�E�C�F�C�G�͓����ɂ͐��藧���Ȃ��̂ŁC�����ł���B
�@����āCf ( c )��0�ƂȂ�c�i��0�j�͑��݂��Ȃ��B���w���@�B
�@���Ȃ킿�C
x��0�̂Ƃ��Cf ( x )��0
�@�ȏ���C���@f ( x ) �́C
�@�@�@�@�@�@�@�@�@f ( x )��0 �ix��0�̂Ƃ��j�C�@f ( 0 )�͔C��
�@����f ( x )�͏�Ɂi���j�����B���������ΐ��藧���Ƃ��킩��B
�i���j�@f ( x )��x
�@�@�@�܂��́C�@f ( x )��0 �ix��0�̂Ƃ��j�C�@f ( 0 )�͔C��

[�l����]�@
���̈Ӗ����킩��ɂ����̂ł����C
�@�@�un���P���܂����߂��Ƃ��C�ǂ��r�ɂ��Ă����������藧�悤�ɂł���v
�Ƃ������Ƃł��B�͂��߁C�u���݂���v���������Ǝv������ōl���Ă��܂������C�ǂ��������̂悤�ŁC
�u���݂��Ȃ��v���Ƃ�n�ɂ��Ă����w�I�A�[�@�ŏؖ����邱�ƂɂȂ�܂��B����͑�������E�E�B
[��]�@
 �@
�@
�@�Ƃ����B�@
|
�@ |
��n��k�{1�̂Ƃ��̋�Ԃ�ݒ肷��B �@���ƂŕύX�����邽�߁Cq�Ɂu�L�v�����Ă����B |
�@���܁Cpk+1 ��qk+1'�@������C��ԁi pk+1 �Cqk+1'�@�j�ɗL�����͑��݂���B