2008年 日本ジュニア数学オリンピック 問題と解答
2008年1月14日 試験時間3時間
|
1. 次の計算をせよ。 877×879-121×123 |
[解答]
工夫するより普通に計算した方が早い。
877×879-121×123=770883-14883
=756000 ・・・・・・(答)
[別解]
121=x,123=yとおくと,←和が1000になる2数に着目
877×879-121×123=(1000-y) (1000-x)-xy
=1000000-1000 ( x+y )
=1000000-1000×244=756000 ・・・・・・(答)
|
2. 1004×1005×1006×・・・×2008は2で最大何回割り切れるか。 |
[考え方]
数を実際に2で割り,その商をさらに次々と2で割っていきます。割り切れない数は無視して,割った数
が何個あるかを調べれば,それが答えになります。
例えば,4×5×6×7×8の場合を考えると,次のように6回割り切れることになります。
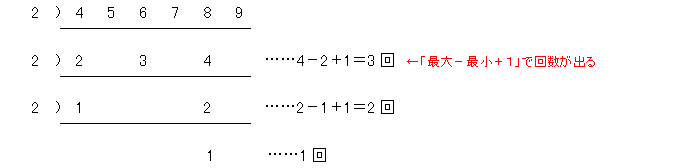
[解答]
1004から2008までの数についても上と同様に,次々と2で割っていく。
商は最小と最大のみがわかれば個数もわかるので,それのみ記入する。
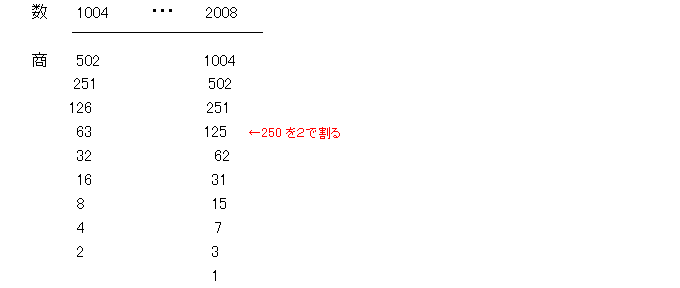
上図のように,合計10行の2で割る計算をして,これですべてである。
求める答えは,図の左の列の数に「-」をつけた数と右の列の数との和に9を加えたものである。
和が-1になる2数が7個あるので, ↑「最大-最小+1」の1を加える部分が9回
1004+(-7)+9=1006 ・・・・・・(答)
|
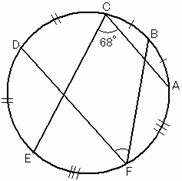
3. 円周上に6点A,B,C,D,E,Fをこの順に,弧ABと弧BC,弧CDと弧DE,弧EFと弧FA の長さがそれぞれ等しくなるようにとる。∠ACE=68°のとき,∠BFDの大きさを求めよ。 ただし,図は正確とは限らない。 |
[考え方]
弧に対する円周角の大きさを考えます。
[解答]
EF,AFを結ぶと,
∠AFE=180°-68°=112°
弧BDの長さは弧ABEの長さの半分だから,対する円周角も半分で,
![]()
|
4. 太郎君は,1000円札と100円玉と10円玉と1円玉を1枚ずつ持って買い物に行き,ある 品物を買って,4枚すべてを支払いに用いた。品物の価格として考えられる値は何通りあるか。 ただし,太郎君は,自分の支払うお金と釣り銭とに共通のものがないような支払い方のうち, 釣り銭を渡された後の手持ちのお金の枚数が最小になるような支払い方を選ぶものとする。 なお,釣り銭は枚数が最小になるように渡されるものとする。また,お釣りが0円であることも ある。 |
[考え方]
太郎君は,価格よりも多い金額を払うことで手持ちの小銭を軽くしたい,と考えています。
例えば,品物の価格が,
・600円の場合, 1000+100+10+1=1111円を支払って,お釣りが511円だから,500円玉,10円
玉,1円玉が1枚ずつ戻る。これは「自分の支払うお金と釣り銭とに共通のものがない」という支払い
方になっていないので,適さない。
・606円の場合, 1000+100+10+1=1111円を支払って,お釣りが505円だから,500円玉,5円玉
が1枚ずつ戻る。←釣り銭は枚数が最小になるように渡されるので,この場合100円玉や1円玉では来ない。
「自分の支払うお金と釣り銭とに共通のものがない」という支払い方になっており,しかもこれは,他の
どの支払い方よりも後の手持ちの枚数が少ない。ので適する。
↑手持ちの枚数は3枚。1000円札1枚や1001円で支払うと,これよりも手持ちが多くなってしまう,ということ。
[解答]
支払うお金と釣り銭とに共通のものが存在しないから,釣り銭は100円玉,10円玉,1円玉では返って
こない。よって釣り銭がある場合,これらが5枚集まって500円玉,50円玉,5円玉のどれかとなる。
ただし,それぞれが2枚以上になると,1000円札または100円玉または10円玉が含まれてしまう。
よって,釣り銭としてあり得るのは,500円玉,50円玉,5円玉が高々1枚含まれる場合で,
0円 5円 50円 55円 500円 505円 550円 555円
である。
(答) 8通り
|
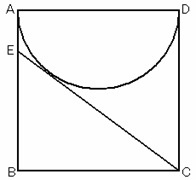
5. 一辺1の正方形ABCDがある。ADを直径とする円をOとし,辺AB上の点Eを,直線CE がOの接線となるようにとる。このとき,三角形CBEの面積を求めよ。 |
[考え方]
BEがわかれば面積もわかります。
[解答]
右図で,AE=EF,CD=CF=1
∠COE=90°だから,△OEF∽△COF
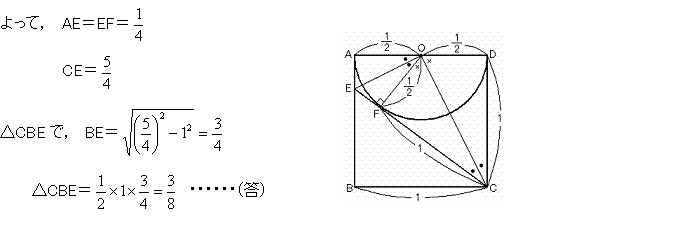
|
6. ある剣道大会は参加者が6人で,どの人も自分以外の5人と1回ずつ対戦した。また, 勝った試合の数は全員異なった。このとき,試合の勝敗の組合せとして考えられるものは 何通りあるか。ただし,引き分けは起こりえないものとする。 |
[考え方]
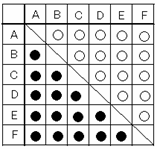
まず6人の星取表をつくってみます。
[解答]
|
勝った試合の数は全員異なるので,その勝ち数は, 0,1,2,3,4,5 である。6人を勝ち数の多い順にA,B,C,D,E,Fとして 成績表をつくれば,右図のように1種類に決まる。 試合の勝敗の組合せは,A~Fに6人を当てはめる場合 の数に等しいから, 6×5×4×3×2×1=720(通り) ・・・・・・(答) |
|
|
7. 正の整数の組 (a,b,c) で,a,b,cの最小公倍数が720となるものはいくつあるか。 ただし,3つの数の並ぶ順番が異なる組は区別して考える。 |
[考え方]
例えばa=23×3,b=22×32の最小公倍数は,指数の大きい方を取って,23×32となります。
こういう考え方でa,b,cの形を決めていきます。a,b,cを区別するというのでややこしく見えますが,
これがかえって求めやすくなるようです。
[解答]
720=24×32×5
a,b,cは2,3,5のいずれかまたはすべてを因数にもち, a,b,cのいずれかの因数の中に24,32,5
を含む。また,それ以外の因数はみな24,32,5の次数を超えない
↑例えば, a=23×3×5,b=22×32,c=24×32×5 の最小公倍数は24×32×5=720となる。
よって,a,b,cの選び方は,2,3,5の指数の組合せを求めればよい。
2の累乗の因数の選び方は, 指数を0~4から3つ選び,このうち4を少なくとも1つ含む場合だから,
53-43=61(通り)
3の累乗の因数の選び方は, 同様に,
33-23=19(通り)
5の累乗の因数の選び方は,
23-1=7(通り)
よって,a,b,cの組の総数は,
61×19×7=8113(通り) ・・・・・・(答)
|
8. ある中学校でチューリップの球根を植えることになった。全員少なくとも1個は植えること にし,同じ学年の生徒は同じ個数の球根を植えることにすると,植える球根の個数としてあり うる100より小さい数は6個あり,小さい方から2つは52,64であった。 このとき,中1,中2,中3の人数の組合せとしてありうるものを求めよ。 |
[考え方]
球根の個数が52の場合はひとり1個ずつ植えたときだから,これで合計人数が52とわかります。
次に,3学年が1個,1個,2個植えた場合,1個,1個,3個植えた場合など,いろいろなケースがあり
ますが,これらが100より小さい5個の数に決まるよう人数をしぼっていく,という考え方をします。
[解答]
中1,中2,中3の人数を,順不同でx,y,z(x≦y≦z)とし,それぞれが植えたひとり当たりの本数を
順にa,b,cとする。
植えた球根の個数52は,(a,b,c)=(1,1,1) のときだから,
x+y+z=52 ・・・・・・①
植えた球根の個数64は,(a,b,c)=(2,1,1) のときだから,
2x+y+z=64 ・・・・・・② ←2番目の個数なので,最も人数の少ない学年だけが2個植えた場合。
①,②より, x=12,y+z=40 ←xがわかった。あとはy,zがわかればいい。
ここで,x≦y≦zだから,12≦y≦20
また,(a,b,c)=(3,1,1) の場合,
3x+y+z=36+40=76 ←それぞれ個数が確定する。
(a,b,c)=(4,1,1) の場合,
4x+y+z=48+40=88
(a,b,c)=(1,2,2) の場合,
x+2(y+z)=12+80=92
以上より,球根の個数としてありえる100より小さい数は,
52,64,76,88,92 ・・・・・・(*)
と,あともう1つ(65以上)である。
さらに,考えられるa,b,cの組をいくつか挙げていくと,植えた個数は,
(a,b,c)=(1,2,1) の場合, x+2y+z=52+y (64以上72以下)
(a,b,c)=(2,2,1) の場合, 2x+2y+z=64+y
(a,b,c)=(3,2,1) の場合, 3x+2y+z=76+y
これらは差が12だから,このうちの2つ以上が(*)の数になるには,
52+y=64 y=12 このとき,z=28
これ以外に無い。
よって, x=12,y=12,z=28 ←この値が問題の条件を満たすことの確認が必要だが,
(答) 12人,12人,28人 答えのみ記入の問題なので,それは省略。
|
9. 2008人の男子と2008人の女子が集まってプレゼント交換をする。男子は花束を,女子は チョコレートを1つずつプレゼントとして用意する。全員で円形に並んで内側を向き,1回合図が あるごとに同時にプレゼントを右隣の人に渡す。男子はチョコレートを,女子は花束を受け取っ たらその時点で円から抜けることにする。 このとき,全員が円から抜けるまでに必要な合図の回数は最大で何回か。 |
[考え方]
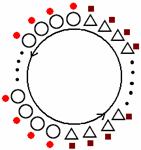
男子を○,女子を△として8人の場合を調べてみよう。花束を●,チョコレートを■とする。
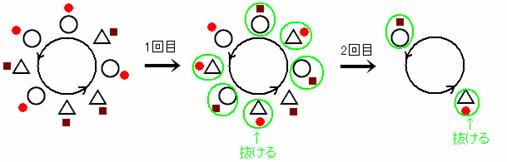
1回に抜ける人数は男女同じ。男女の隣り合わせが少ない方が回数が多くなりそうだと予測できる。
[解答]
輪の中に,ある男子の右隣には女子Aが,ある女子の右隣には男子Bが並ぶという場所が必ずあり,
1回の合図でAとBが円から抜け出ることになる。
よって,1回の合図で円から抜ける人数は少なくとも2人である。
また,1回の合図で男子がa人,女子がb人抜けたとすると,a個のチョコレートとb本の花束がなくな
り,残りの男子2008-a人が2008-b本の花束を持っている。
2008-a=2008-bより,a=b
よって,1回の合図で抜ける男女の人数は等しい。←この説明は必要ないかもしれない。
1回の合図で男女1人ずつ抜けていくとすると,全員が抜けるには2008回かかる。これが最大である。
|
このような場合があることを示す。 右図のように,男子2008人,女子2008人がそれぞれ連続するように 並べば,1回の合図で左端の男子と左端の女子が抜け,この操作が 2008回繰り返されて全員が抜けることになる。←こういう極端な場合が最大。 (答) 2008回 |
|
|
|
[考え方]
|
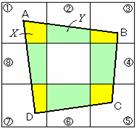
Yは4つの台形の面積の和となる。この台形の高さは1なので, 上底と下底を文字でおけば面積が表せる。困るのはXの方で, ひとまず4つの四角形をそれぞれ三角形に分割して考えてみる。 |
|
[解答]
図のようにa,b,x,yを定める。四角形APQBにおいて,
黄色の部分の面積の和をA1,緑の部分の面積をB1とすると,

よって, A1<B1 ←示せた。
同様に,四角形BQRC,CRSD,DSPAにおいても黄色と緑の部分の面積を順に,
A2,B2,A3,B3,A4,B4とすると,
A2<B2,A3<B3,A4<B4 ←上と全く同じこと。
となる。
X=A1+A2+A3+A4,Y=B1+B2+B3+B4
A1+A2+A3+A4<B1+B2+B3+B4
だから, X<Y ←何だか簡単に示せた。何か落ちがあるのだろうか・・?
|
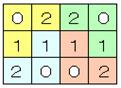
11. m,nは正の整数とする。m×nのマス目の各マスを赤,青,黒のいずれかの色で塗り, 次の条件をすべてみたすようにしたい。 ・どの赤いマスもちょうど1つの青いマスとちょうど1つの黒いマスに接している。 ・どの青いマスもちょうど1つの黒いマスとちょうど1つの赤いマスに接している。 ・どの黒いマスもちょうど1つの赤いマスとちょうど1つの青いマスに接している。 ただし,相異なる2つのマスが辺を共有しているとき,それらは接しているという。 このとき,以下の問いに答えよ。 (1) m=3,n=4の場合に,上記の条件をみたす塗り方を1つ求めよ。(答のみでよい) (2) 上記の条件をみたすように塗ることのできる(m,n)の組をすべて求めよ。 |
[考え方]
|
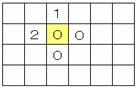
赤,青,黄を0,1,2とすると,例えば「0」と隣り合うマス目には,右図の ように0,0,1,2が書かれる。このように数字を次々と書いていく。 (2) いくつか実験してみて,法則を発見するしかない。(1)の結果を見て, 0,1,2を書き入れた個数が同じであること,(1)の図を対称に折り返し たものを重ねると,その図も条件をみたすこと,などに着目しよう。 何となく答えは予想できても,その理由を示すのが難しい・・。 |
|
[解答]
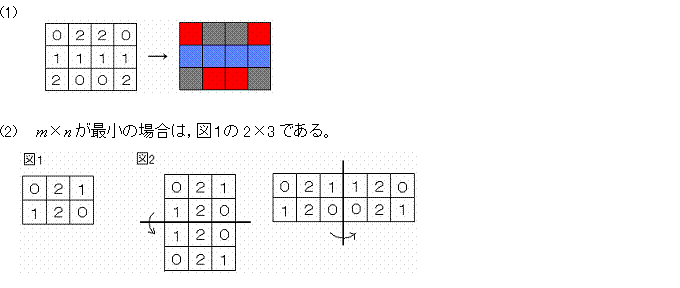
この図を外側の線を軸に折り返した図をつくると,図2のようにできた図形も条件をみたす。
この操作を繰り返すことにより,条件をみたす図を次々とつくることができる。このときの(m,n)の組
は, (2s,3t)または(3t,2s) s,tは自然数 ←これが答えになりそう,と予測できる。
である。
|
次に,上に挙げたもの以外にはないことを示す。←これがややこしい。 いま,条件をみたす1つの図形において,「0」のマス目に着目する。 このマス目に接するマスの中には「1」と「2」のマスが必ず1つずつあるの で,この3つのマスに同じ色をつける。例えば,(1)の図は右のようになる。 |
|
このとき,次が成り立つ。
〔その1〕 どのマスにも色が付けられ,重複はない。
(証明) 色が付いていないマスがあったとすれば,そのマスには「1」か「2」が書かれており,
そのマスは「0」のマスと接していないことになる。これは矛盾。←「背理法」という証明法。
また,重複があったとすれば,「1」または「2」のマスが2色以上で塗られることになるが,
そのマスに接する「0」のマスが2つ以上あることになる。これも矛盾。←これも「背理法」。
この結果,条件をみたす図は,0,1,2の3マスのL字型を組み合わせてできたものである。
〔その2〕 2個のL字型を組み合わせるとき,必ず2×3の長方形になる。
(証明) 1つのL字型の右上のマスにもう1つのL字型が入るとき,次の4つの場合がある。
a,bは1または2で異なる数。
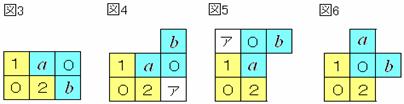
図4では,アの横のラインから,アは1か2であるが,アの上の「0」に「1」または「2」が2個接し
てしまう。図5でも,アの縦のラインから,アは1か2であるが,アの右の「0」に「1」または「2」が
2個接してしまう。図6では,中央の「0」に2個の「1」が接している。
よって,図4~図6の場合はあり得ない。
最後に,条件をみたす図は2×3の長方形を規則正しく並べたものであることを示す。
2×3の長方形の1つに接する長方形が規則正しく並んでいないのは,回転や反転したものを除いて
次の3つの場合である。←カドの「0」にはさらに0が隣り合うので,これをカドにする長方形を考える。
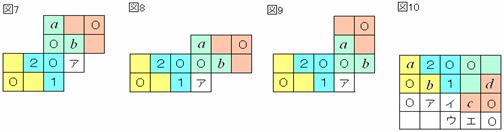
図7では,アには0が入り,アの上のbに2個の「0」が接してしまう。
図8,9では,アには0が入り,アの横の「1」に2個の「0」が接してしまう。
図10では,ア,イは0でないのでウが長方形のカドとなり「0」。するとエも長方形のカドで,
右が0だからエは1か2。どちらの場合も2個の「0」が接してしまう。
よって,図7~図10の場合はあり得ない。
↑これほど面倒な調査をしないといけないのか・・?ほかにうまい解がありそう。
これで条件をみたす図は,2×3の長方形を同じ方向に規則正しく並べたものしかないことが
示された。←確認モレが大いにあるかもしれない。 (答) (2s,3t),(3t,2s) ただし,s,tは自然数